JP / EN

Broyden Tridiagonal Function

03. Large-scale Scalability Benchmark

\[ f_i(\boldsymbol{x}) = (3 - 2x_i)x_i - x_{i-1} - 2x_{i+1} + 1 = 0 \] \[ (i = 1, \dots, n, \quad x_0 = x_{n+1} = 0) \]

Structure and Scalability

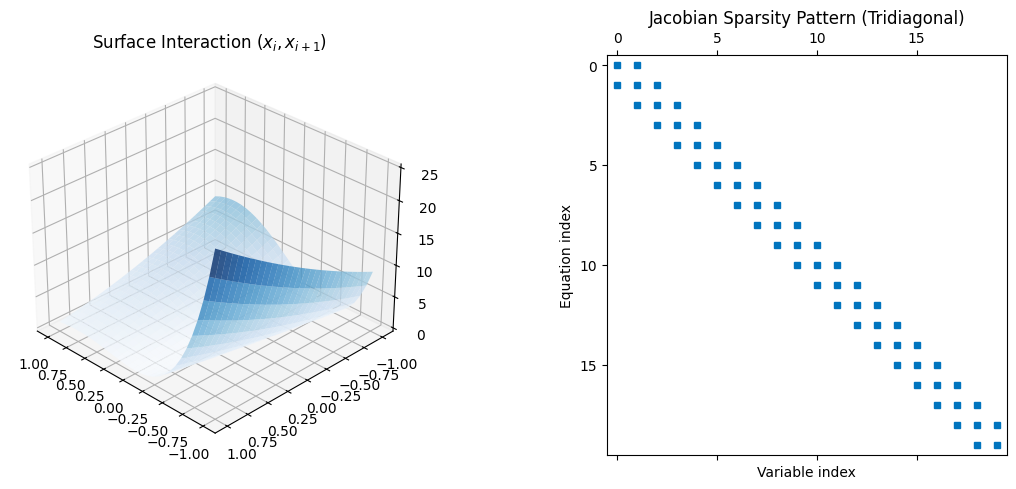
Broyden Tridiagonal Function Analysis

Fig: 2D cross-section (left) and sparsity pattern of the Jacobian (right).
The left plot shows the interaction between adjacent variables. The right plot illustrates the "Tridiagonal" sparse structure, which allows for efficient computation even as the number of variables $n$ increases.

Significance

This function is essential for testing algorithms designed for large-scale systems, as it mimics the matrix structures found in discretized boundary value problems and other physical phenomena.

Results

The following shows the results of solving the Broyden tridiagonal function (2-variable) using Newton's method.

Instead of direct programming, the analysis was performed using "SPICE-oriented approach," a methodology based on the unconventional idea of describing equations as circuits and solving them with a SPICE circuit simulator. Since this system of equations has multiple solutions, it may converge to different points depending on the initial values used in Newton's method. If given the opportunity, I would like to explore whether multiple solutions can be identified using the Homotopy method or other advanced techniques.

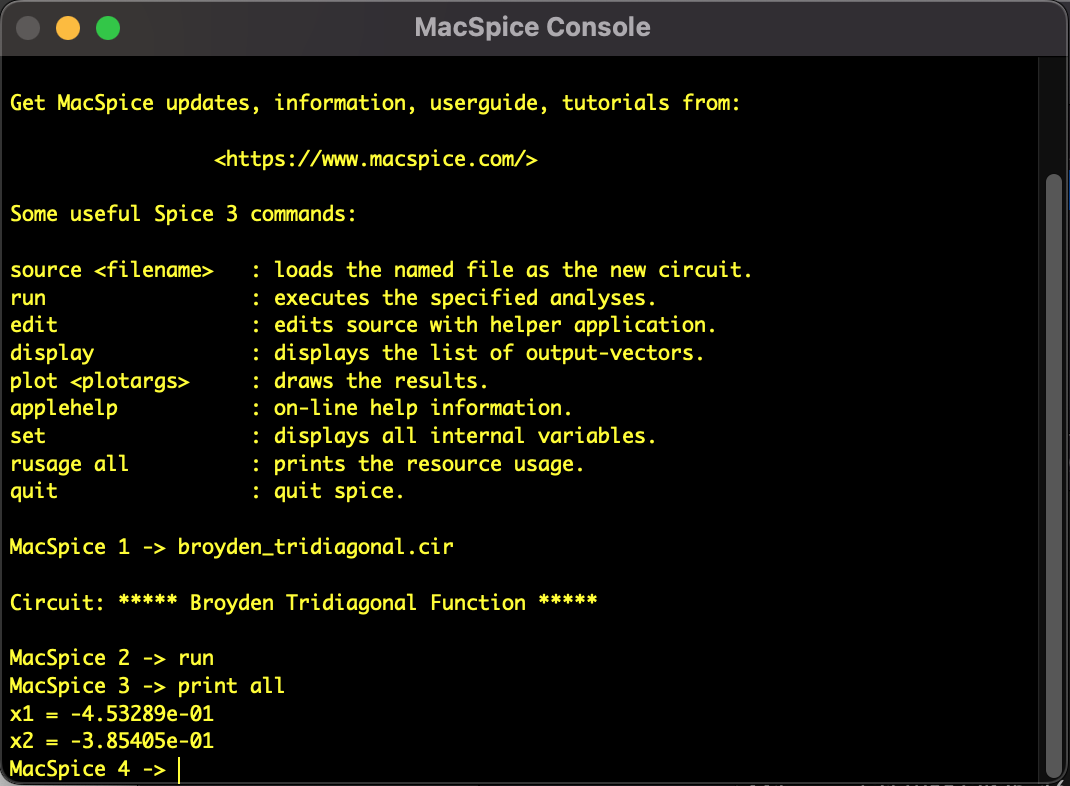
SPICE Analysis Result

Fig: Analysis result of the Broyden tridiagonal function using SPICE-oriented approach.

Analysis Environment

  • SPICE: Mac SPICE3
  • PC: MacBook
  • OS: macOS Monterey 12.7.6
  • CPU: 1.2GHz Dual-Core Intel Core m5
  • Memory: 8GB

Given the computational scale, convergence is achieved instantaneously on modern PC environments; therefore, detailed measurement of computation time has been omitted.