Broyden Tridiagonal Function

ブライデン三対角関数は、変数の数 $n$ を自由に設定できるスケーラブルな方程式系です。各要素 $f_i$ が隣接する変数のみに依存するため、ヤコビ行列が「三対角行列（Tridiagonal Matrix）」という疎な（スパースな）構造を持ちます。

この特性は、大規模な連立方程式を解く際のメモリ効率や計算速度のベンチマークとして非常に有用です。特に、準ニュートン法（Broyden法）の効果を測定する際によく用いられます。

境界値問題の離散化など、物理現象を網羅的に計算する際に現れる行列構造に近いため、実務的なアルゴリズムの実装において避けては通れないテストケースの一つです。

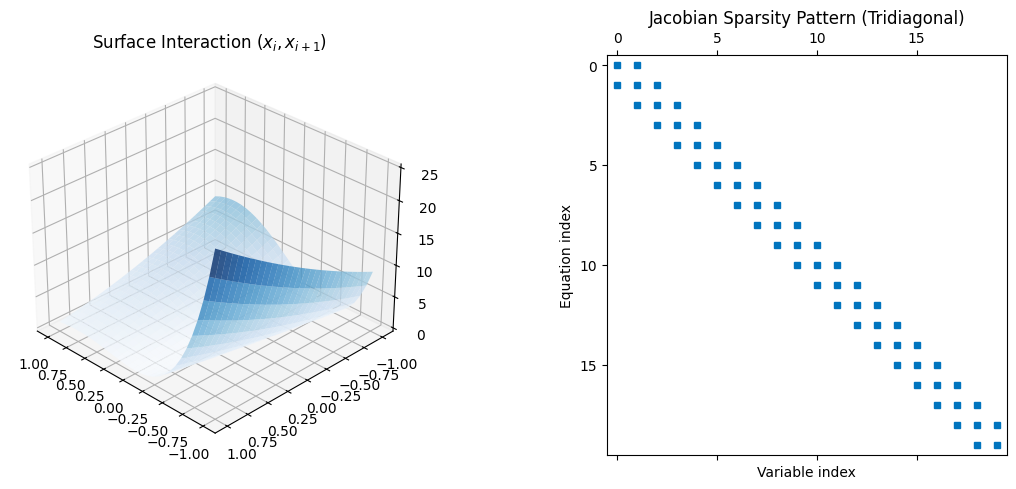
図：ブライデン三対角関数の2変数断面図（左）と次元数増加による計算コスト推移（右）。
左図は、隣接する変数 $x_i, x_{i+1}$ 以外を固定した際の形状で、比較的穏やかな非線形性を示しています。 しかし、右図が示す通り、変数の数 $n$ を増やしても三対角行列というスパース（疎）な構造が維持されるため、大規模なシステムにおいても計算量が爆発的に増えることなく、効率的なアルゴリズム検証を可能にします。

ブライデン三対角関数（2変数）をニュートン法で解いた結果を示します。

今回は直接プログラミングするのではなく、式を回路で記述して回路シミュレーターSPICEで解くという逆転的発想に基づいた方法論である「SPICE指向型解析法」を用いて解析を行いました。 この方程式は解が複数ありますので、ニュートン法の初期値の取り方によっては別の階に収束すると思います。 機会があればホモトピー法などを用いて、複数回が求まるか試してみたいと思います。

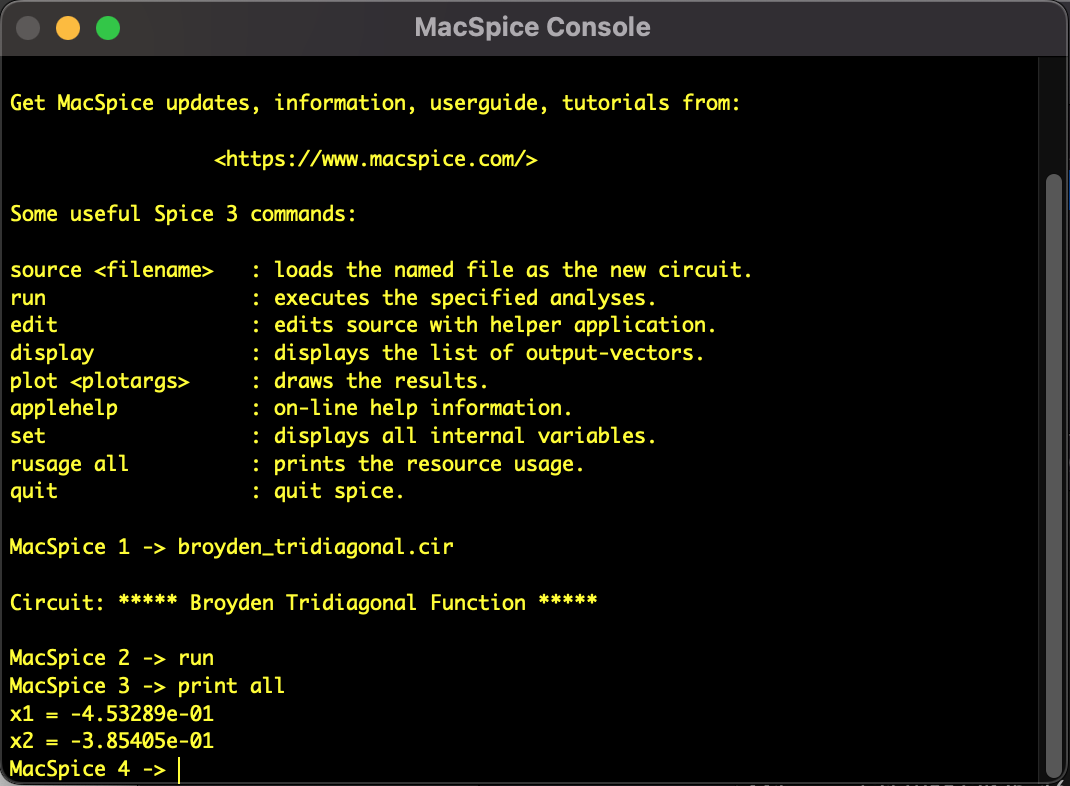
図：SPICE指向型解析法によるブライデン三対角関数の解析結果

解析環境

• SPICE： Mac SPICE3
• PC： MacBook
• OS： macOS Monterey 12.7.6
• CPU： 1.2GHz デュアルコア Intel Core m5
• メモリ： 8GB

この規模の計算では現在のPC環境であれば一瞬で収束するため、詳細な計算時間の計測は割愛いたします。