Lorenz Attractor
2. Lorenz Attractor
Standard parameters: $\sigma=10, \quad \rho=28, \quad \beta=8/3$
Features
A nonlinear differential equation proposed by meteorologist Edward Lorenz as a model of atmospheric convection.
Despite being "deterministic" (containing no random elements), tiny differences in initial conditions grow exponentially over time, resulting in unpredictable behavior. This property is known as the "Butterfly Effect" and has become a landmark concept in Chaos Theory.
Behavior of Solution (Real-time Visualization)
The result of real-time calculation using the Runge-Kutta method (simplified) is rendered in the browser. A beautiful strange attractor resembling a butterfly with two wings appears.
Fig 1: Numerical calculation result by JavaScript (projection onto x-z plane). The orbit circles infinitely but never passes through exactly the same location.
Results
The results of analyzing the Lorenz equations using the trapezoidal method are shown below.
Instead of direct programming, we performed the analysis using the "SPICE-Oriented Analysis Method," a reverse-thinking approach where equations are described as circuits and solved by a circuit simulator.
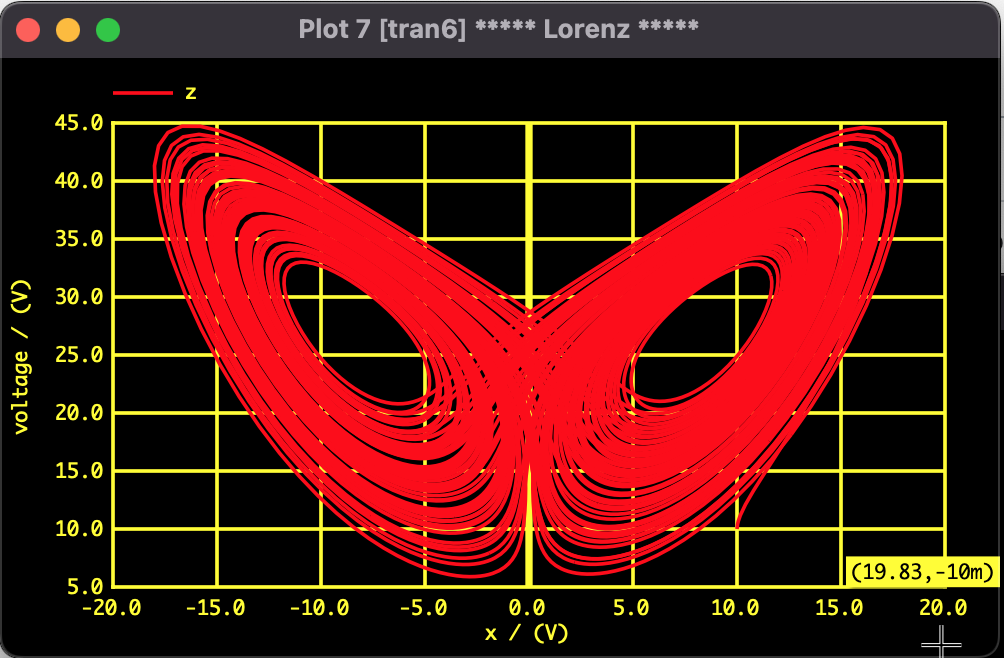
Fig 2: Analysis result of Lorenz Attractor by SPICE-Oriented Analysis Method
Analysis Environment
- SPICE: Mac SPICE3
- PC: MacBook
- OS: macOS Monterey 12.7.6
- CPU: 1.2GHz Dual-Core Intel Core m5
- Memory: 8GB
Since calculation of this scale converges instantly in the current PC environment, detailed calculation time measurement is omitted.