Lorenz Attractor

2. ローレンツ・アトラクタ

\[ \begin{cases} \frac{dx}{dt} = \sigma (y - x) \\ \frac{dy}{dt} = x (\rho - z) - y \\ \frac{dz}{dt} = xy - \beta z \end{cases} \]

Standard parameters: $\sigma=10, \quad \rho=28, \quad \beta=8/3$

特徴

気象学者エドワード・ローレンツが、大気の対流モデルとして提唱した非線形微分方程式です。

この方程式は「決定論的（ランダムな要素がない）」であるにもかかわらず、初期値のごくわずかな違いが時間の経過とともに指数関数的に拡大し、予測不可能な挙動を示します。この性質は「バタフライ効果」として知られ、カオス理論の金字塔となりました。

ブラウザ上でルンゲ・クッタ法を用いてリアルタイム計算した結果を描画しています。二つの翼を持つ蝶のような美しいストレンジ・アトラクタが現れます。

図1：JavaScriptによる数値計算結果 ($x-z$ 平面への投影)。軌道は無限に回り続けますが、決して同じ場所を通ることはありません。

ローレンツ・アトラクタを台形法で解析した結果を示します。

今回は直接プログラミングするのではなく、式を回路で記述して回路シミュレーターSPICEで解くという逆転的発想に基づいた方法論である「SPICE指向型解析法」を用いて解析を行いました。

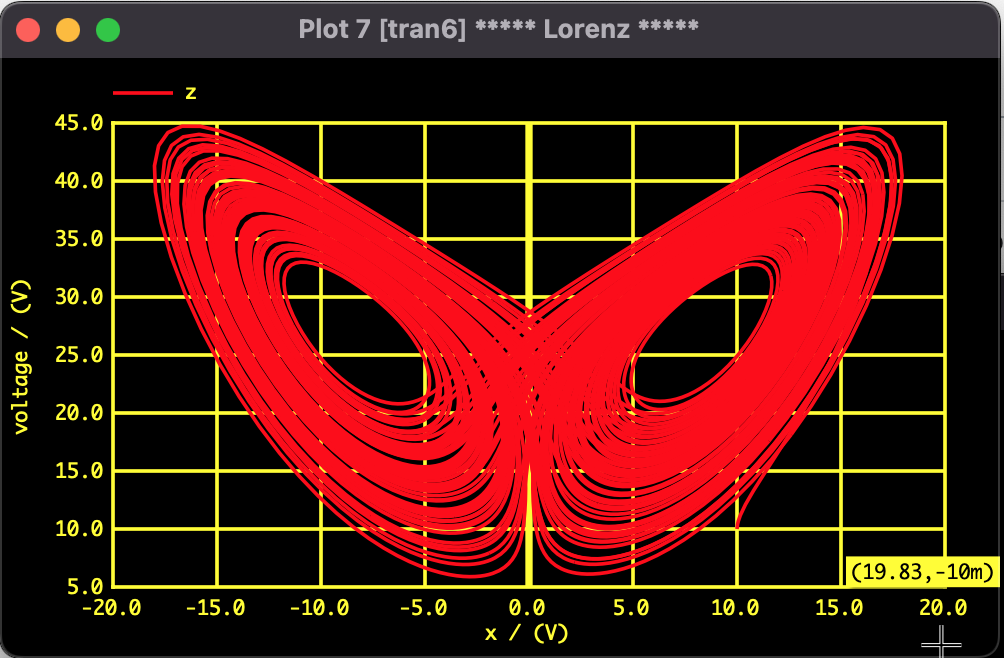
図2：SPICE指向型解析法によるローレンツ・アトラクタの解析結果

この規模の計算では現在のPC環境であれば一瞬で収束するため、詳細な計算時間の計測は割愛いたします。