Powell's Singular Function
02. Testing Robustness against Singularity
Characteristics
The defining feature of Powell's function is that the Jacobian matrix becomes singular (rank-deficient) at the solution $(0, 0, 0, 0)$. This poses a significant challenge for standard Newton methods, which rely on the existence of the inverse Jacobian.
Behavior and Singularity
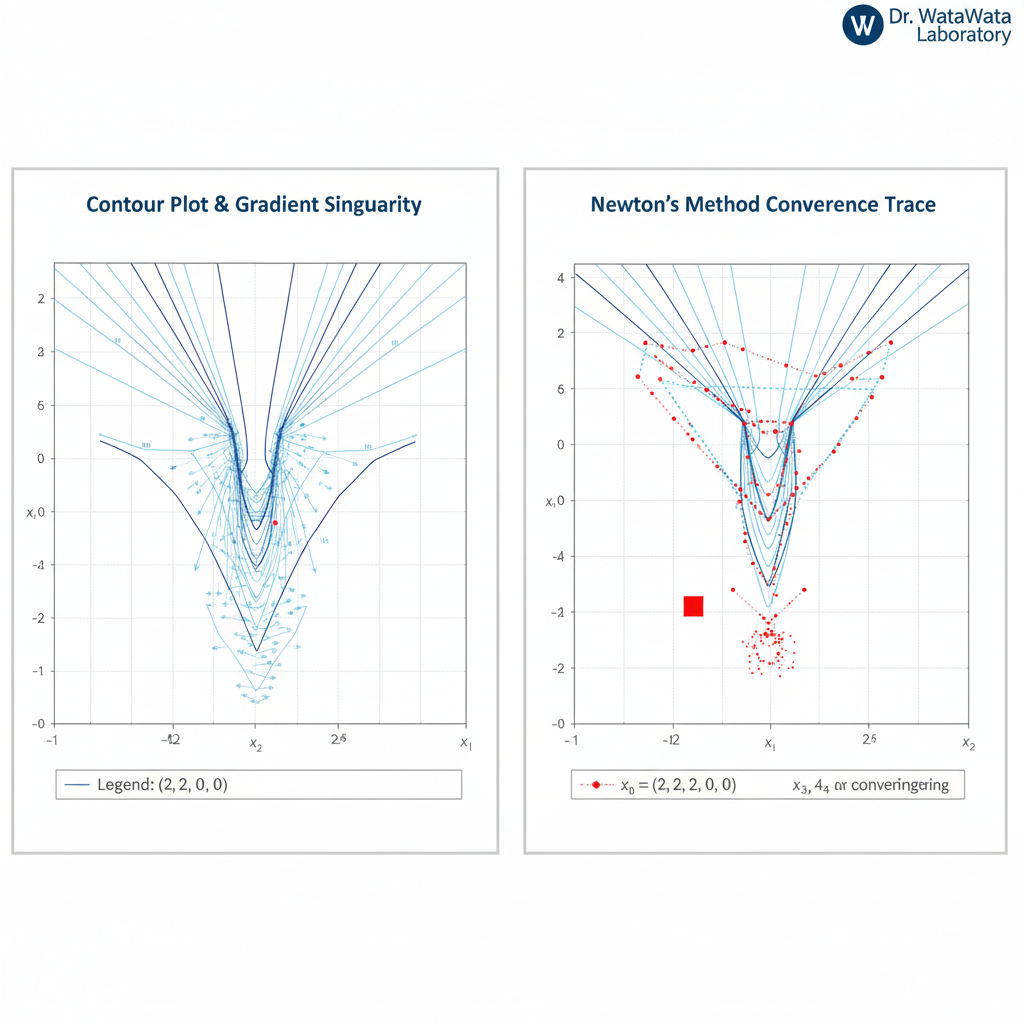
Fig: Contour plot (left) and iteration path (right).
The left figure shows how the contours become extremely elongated near the origin, creating a "singular valley" where gradients vanish. The right figure demonstrates how standard methods stagnate near the solution due to numerical instability.
Results
The following shows the results of solving the Powell's Singular function using Newton's method.
Instead of conventional direct programming, the analysis was performed using the "SPICE-oriented approach," a methodology based on the unconventional idea of describing equations as electrical circuits and solving them with the SPICE circuit simulator.
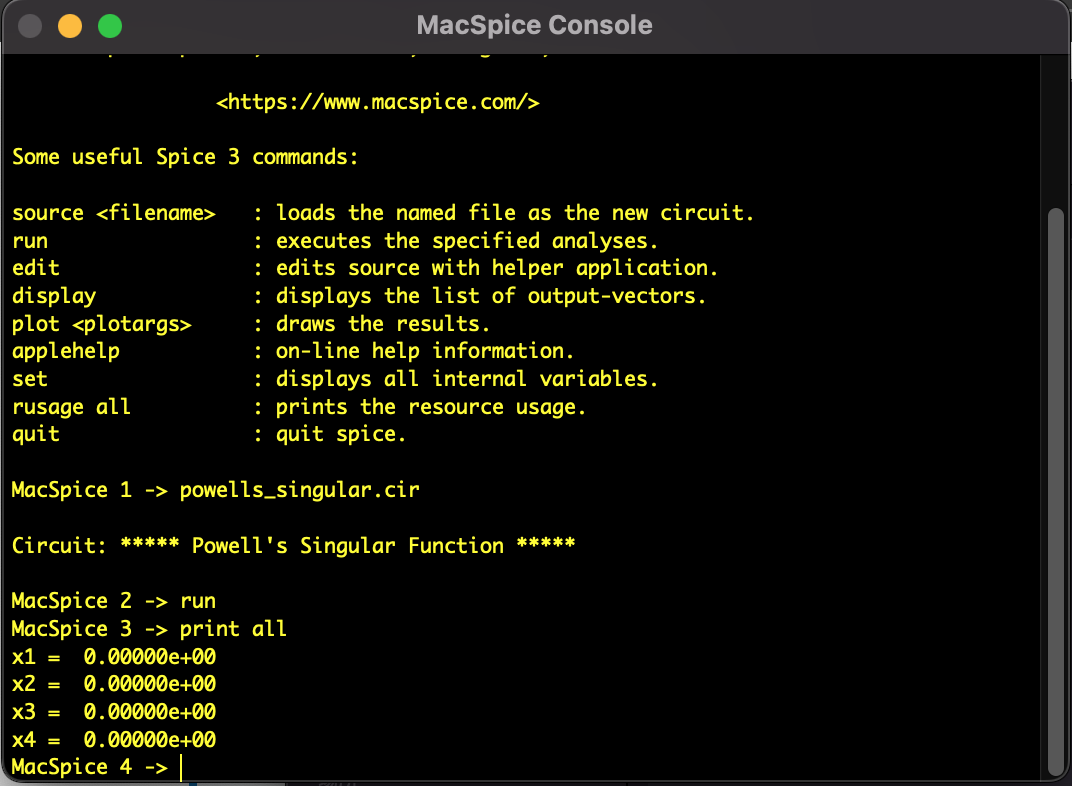
Fig: Analysis results of the Powell's Singular function using the SPICE-oriented approach.
Analysis Environment
- SPICE: Mac SPICE3
- PC: MacBook
- OS: macOS Monterey 12.7.6
- CPU: 1.2GHz Dual-Core Intel Core m5
- Memory: 8GB
Given the computational scale, convergence is achieved instantaneously on modern PC environments; therefore, detailed measurement of computation time has been omitted.