Powell's Singular Function

パウエルの特異関数は、4変数からなる非線形方程式系です。この関数の最大の特徴は、解 $(0, 0, 0, 0)$ においてヤコビ行列が特異（ランク落ち）になる点にあります。

標準的なニュートン法では、ヤコビ行列の逆行列が存在することを前提としているため、この問題では収束速度が著しく低下するか、あるいは計算が破綻します。特異性の高い問題に対するアルゴリズムの頑健性（ロバストネス）を評価するための重要なテストケースです。

この問題は「ヤコビ行列が特異であっても、いかにして解に到達するか」という課題を提示します。信頼領域法（Trust Region Method）やレベンバーグ・マルカート法などの導入を検討する際の試金石となります。

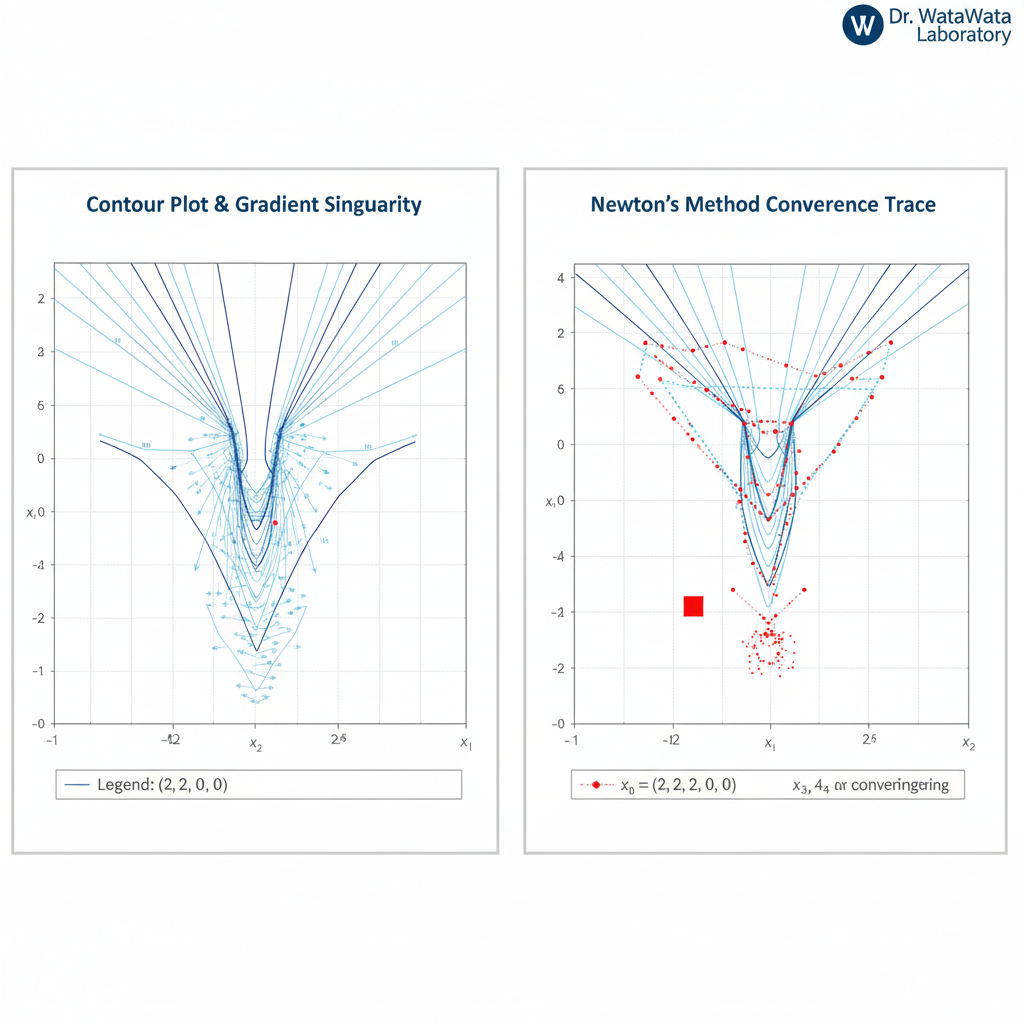
図：パウエルの特異関数における等高線図（左）と反復計算の軌跡（右）。
左図では、解（原点）に近づくにつれて等高線が極端に細長くなり、特定の方向に沿って勾配が消失していく「特異な谷」の様子が確認できます。 右図の反復軌跡では、この特異性の影響でヤコビ行列が不安定になり、標準的なニュートン法が解の付近で足踏みし、収束が著しく停滞する挙動を示しています。

パウエルの特異関数をニュートン法で解いた結果を示します。

今回は直接プログラミングするのではなく、式を回路で記述して回路シミュレーターSPICEで解くという逆転的発想に基づいた方法論である「SPICE指向型解析法」を用いて解析を行いました。

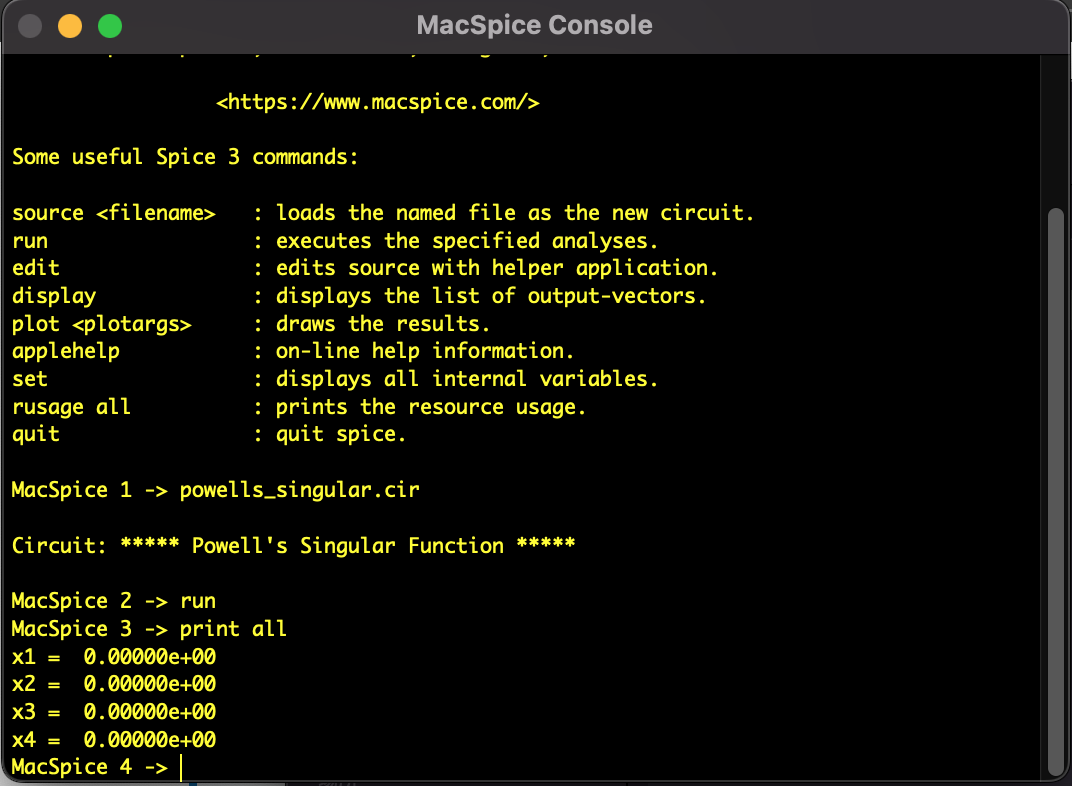
図：SPICE指向型解析法によるパウエルの特異関数の解析結果

解析環境

• SPICE： Mac SPICE3
• PC： MacBook
• OS： macOS Monterey 12.7.6
• CPU： 1.2GHz デュアルコア Intel Core m5
• メモリ： 8GB

この規模の計算では現在のPC環境であれば一瞬で収束するため、詳細な計算時間の計測は割愛いたします。