Chandrasekhar's H-equation
チャンドラセカールのH方程式
Unknown function: $H(\mu)$
Parameter: $c$ (Albedo, $0 \le c \le 1$)
概要
回路シミュレータ「SPICE」が持つ、強力な「非線形方程式ソルバー」としての能力を試すため、天体物理学(輻射輸送論)などで現れる有名な積分方程式「チャンドラセカールのH方程式」を解いてみました。
式中に $\mu$ と $\mu'$ が出てきますが、このダッシュ($'$)は微分を表すものではありません。
- $\mu$:いま値を求めようとしている「特定の方向」。定数として扱います。
- $\mu'$:積分計算のために $0$ から $1$ まで変化させる「別の方向」。
SPICEで解くための「離散化」プロセス
この方程式をコンピュータ(SPICE)で解くためには、式の中に含まれる「積分」を「有限個の足し算」に変換し、連立方程式の形に書き下す必要があります。
ここでは、その導出過程をステップ・バイ・ステップで解説します。
元のチャンドラセカールのH方程式の右辺にある積分項(インテグラル)に注目します。ここを $I(\mu)$ と置きます。この $I(\mu)$ を、和の形 $\sum$ に直すことが目標です。
\[ I(\mu) = \int_0^1 \frac{H(\mu')}{\mu + \mu'} d\mu' \]数値積分の強力な手法である「ガウス・ルジャンドル求積法」を使います。この公式は、積分区間が $[-1, 1]$ のときに使える魔法の公式です。
\[ \int_{-1}^{1} g(t) dt \approx \sum_{j=1}^N w'_j g(t_j) \]($t_j$: ルジャンドル多項式のゼロ点、$w'_j$: 対応する重み)
しかし、今回の積分 $I(\mu)$ の区間は $[0, 1]$ です。このままでは公式が使えないため、変数変換を行います。
積分区間 $[0, 1]$ を、公式が使える $[-1, 1]$ に対応させるため、変数 $\mu'$ を新しい変数 $t$ に置き換えます。
\[ \mu' = \frac{1}{2}t + \frac{1}{2} \]この式を微分すると $d\mu' = \frac{1}{2} dt$ となります。これを元の積分 $I(\mu)$ に代入します。
\[ \begin{aligned} I(\mu) &= \int_{\mu'=0}^{1} \frac{H(\mu')}{\mu + \mu'} d\mu' \\ &= \int_{t=-1}^{1} \frac{H\left(\frac{t+1}{2}\right)}{\mu + \left(\frac{t+1}{2}\right)} \cdot \underbrace{\frac{1}{2} dt}_{d\mu'} \end{aligned} \]積分区間が $[-1, 1]$ になり、末尾に変換係数の $\frac{1}{2}$ が現れました。
区間が $[-1, 1]$ になったので、ガウス求積法の公式を適用して、積分 $\int$ を和 $\sum$ に書き換えます。
ここで、式を簡単にするために、変換後の座標 $t_j$ に対応する元の座標を $\mu_j$ と定義しておきます。
係数 $\frac{1}{2}$ をシグマの外に出しました。
最後に、求めた $I(\mu)$ を元のH方程式に戻し、連続変数 $H(\mu)$ を離散変数 $x_i$ に置き換えると、SPICEに実装すべき最終式が得られます。
\[ x_i = 1 + \frac{c}{2} x_i \sum_{j=1}^N \frac{w'_j \mu_i x_j}{\mu_i + \mu_j} \quad (i=1, \dots, N) \]これで、複雑な積分方程式が、四則演算だけで計算できる連立方程式に変換されました。
計算点の算出 (Python)
「ルジャンドル多項式のゼロ点」を手計算するのは困難ですが、Pythonを使えば一瞬で算出できます。以下のコードで、今回のシミュレーションに使用した $\mu_i$ と重み $w_i$ を生成しました。
import numpy as np
# 1. ルジャンドル多項式のゼロ点 t と重み w_prime を取得(定義域 -1 to 1)
N = 100
t, w_prime = np.polynomial.legendre.legauss(N)
# 2. 今回の積分区間 [0, 1] に変換
# mu : SPICEのノード電圧に対応する変数
# w : 抵抗値計算などに使う重み(0.5倍する)
mu = 0.5 * t + 0.5
w = 0.5 * w_prime
print(f"x1 (min) = {mu[0]:.6f}")
print(f"x100 (max) = {mu[-1]:.6f}")解析結果
100変数の非線形方程式を解くため、SPICEの .DC解析(直流掃引解析) を活用しました。パラメータ $c$ を $0$ から $1.0$ まで連続的に変化させながら解を追跡します。
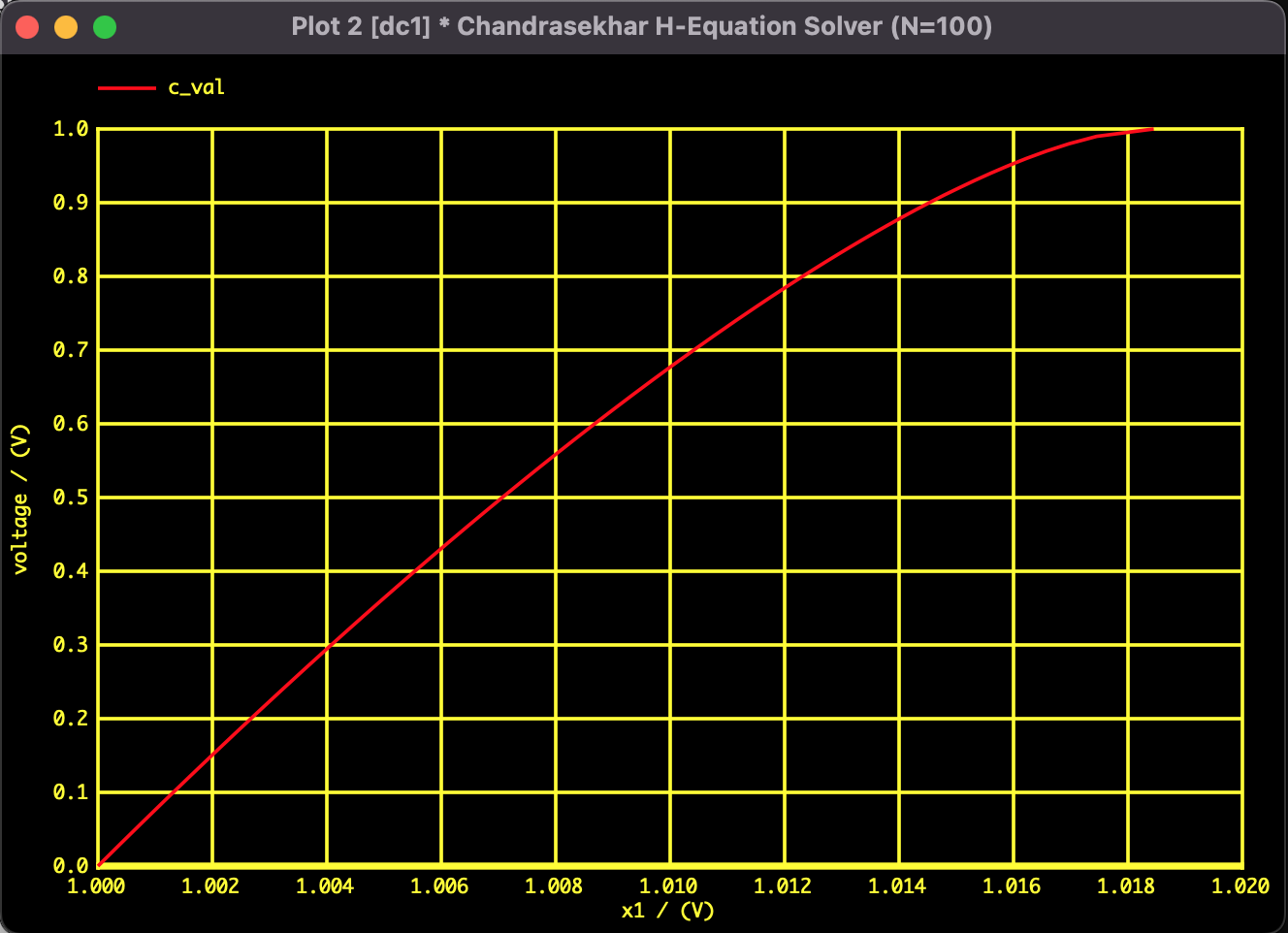
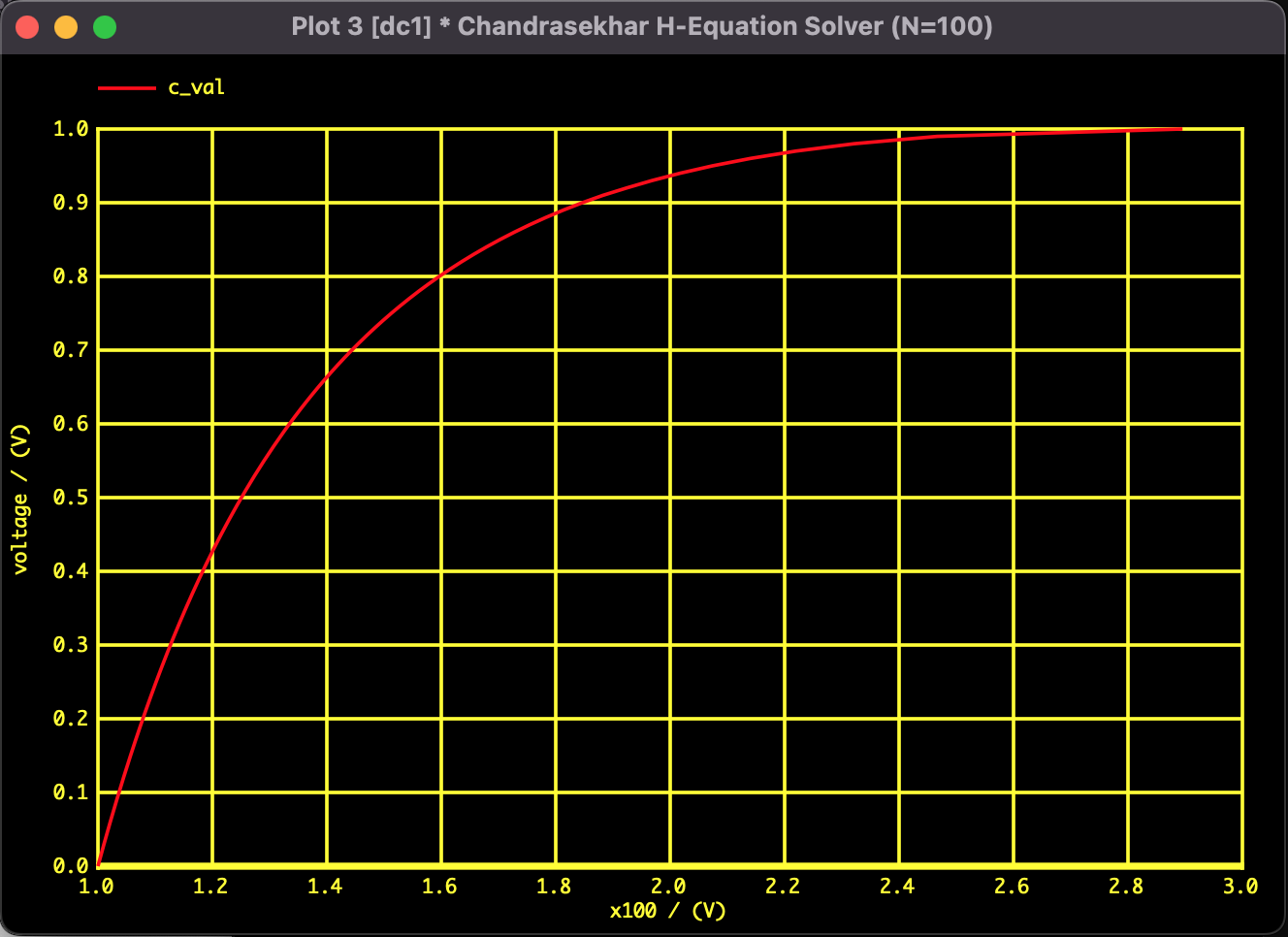
シミュレーションの結果、$c=1.0$ における両端($x_1$ と $x_{100}$)の値は以下の通りとなりました。
| 変数 ($\mu$の位置) | SPICE 実測値 | 理論値 (目安) | 判定 |
|---|---|---|---|
| $x_1$ ($\mu \approx 0$) | 1.01845 | 1.018 | Good |
| $x_{100}$ ($\mu \approx 1$) | 2.89526 | 2.899 | Good |
アナログ回路シミュレータであるSPICEを用いて、100変数の複雑な積分方程式を約 0.1% の精度で解くことに成功しました。
解析環境
- SPICE: Mac SPICE3
- PC: MacBook
- OS: macOS Monterey 12.7.6
- CPU: 1.2GHz デュアルコア Intel Core m5
- メモリ: 8GB
この規模の計算では現在のPC環境であればすぐに計算が完了するため、詳細な計算時間の計測は割愛いたします。