Double Pendulum
二重振り子とカオス・エネルギー保存則
解説:カオスと保存則
二重振り子(Double Pendulum)とは、振り子の先にもうひとつの振り子を連結した物理系です。非常に単純な構造でありながら、その挙動は初期条件に対して極めて敏感であり、予測不可能な「カオス(Chaos)」を示す典型例として知られています。
エネルギー保存則による検証
この系における重要な物理法則が「力学的エネルギー保存則」です。摩擦や空気抵抗を無視できる理想的な環境下では、運動エネルギー $K$ と位置エネルギー $U$ の和 $E$ は、どんなに激しく動き回っても常に一定でなければなりません。
数値シミュレーションにおいては、この $E$ が時間経過とともに変化しないことが、計算精度(シミュレータの信頼性)を保証する最も強力な指標となります。
シミュレーションと支配方程式
以下のデモで、初期値を水平位置($\pi/2$)とした際のカオス的な挙動を確認できます。
長さ $L_1, L_2$、質量 $m_1, m_2$ の二重振り子の運動方程式(ラグランジュ形式)は以下の通りです。この連立2階非線形微分方程式を数値的に解くことで、上記の動きを再現しています。
本解析では以下の物理定数を使用しました。
- $m_1 = 1.0$ [kg], $m_2 = 1.0$ [kg]
- $L_1 = 1.0$ [m], $L_2 = 1.0$ [m]
- $g = 9.8$ [m/s$^2$]
運動方程式(Equations of Motion)
定義式(Definitions)
速度 $\omega$ と角度 $\theta$ の関係式(数値積分における拘束条件)は以下の通りです。
結果
二重振り子を台形法で解析した結果を示します。
今回は直接プログラミングするのではなく、式を回路で記述して回路シミュレーターSPICEで解くという逆転的発想に基づいた方法論である「SPICE指向型解析法」を用いて解析を行いました。
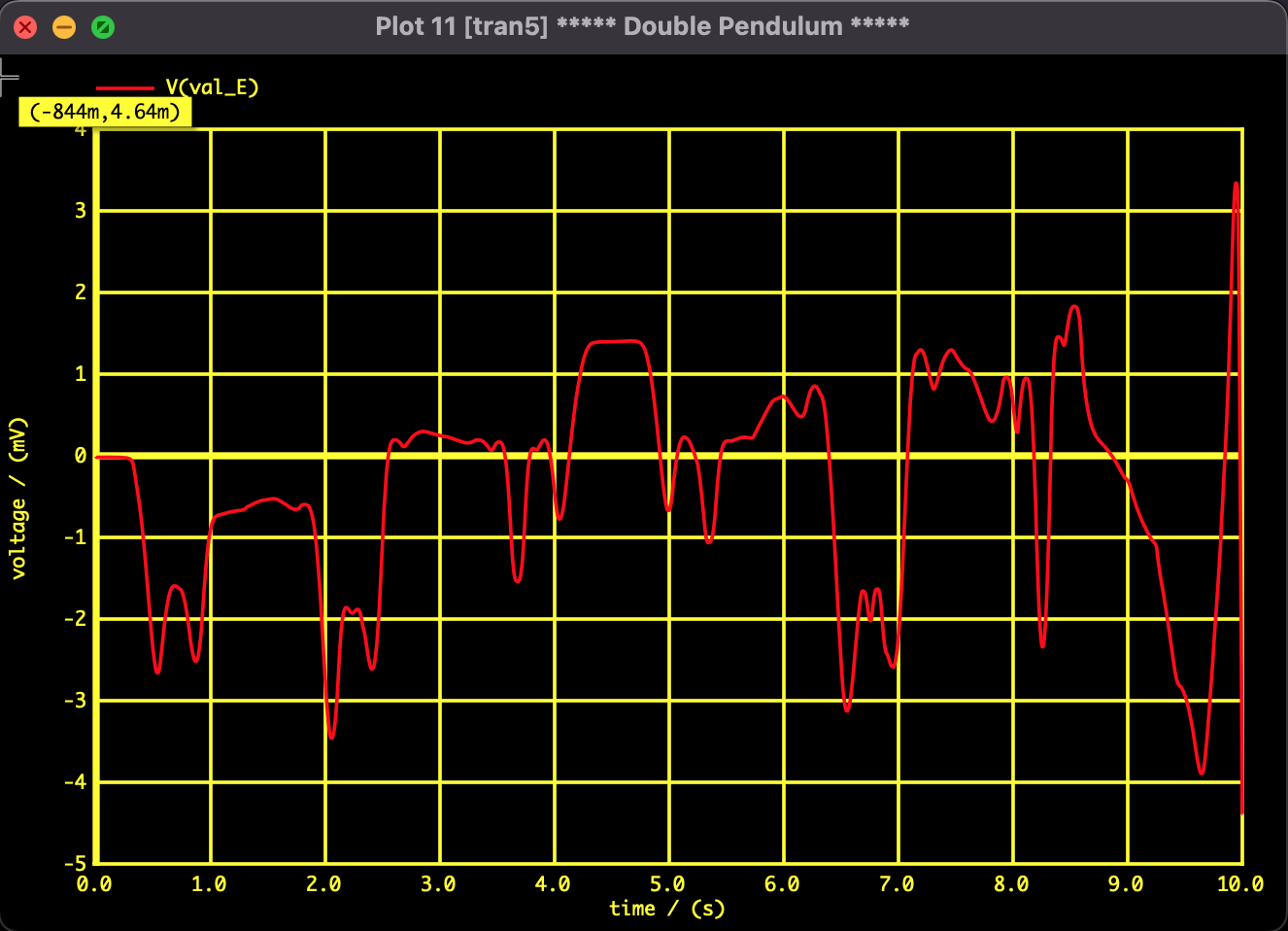
図1:$\theta_1$ と $\theta_2$ の相関プロット(リサージュ図形)。単純な周期運動ではなく、複雑に絡み合うカオス特有の軌道が確認できる。
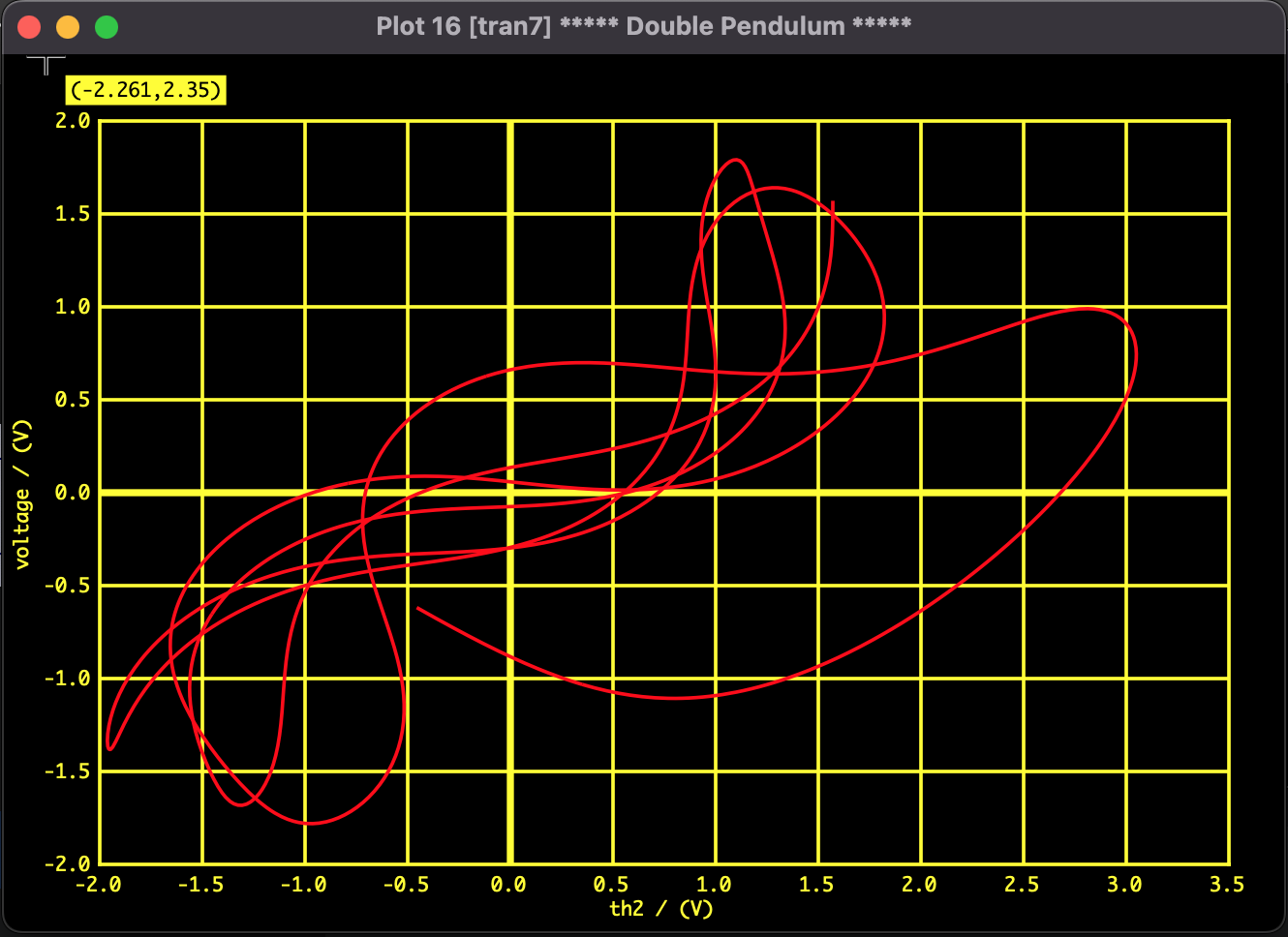
図2:全エネルギーの時間変化。縦軸の単位は [mV](ミリボルト/ミリジュール相当)であり、全体のエネルギー規模(約30J)に対して誤差は0.01%以下に収まっている。これにより、本数値解析モデルの高い計算精度が証明された。
解析環境
- SPICE: Mac SPICE3
- PC: MacBook
- OS: macOS Monterey 12.7.6
- CPU: 1.2GHz デュアルコア Intel Core m5
- メモリ: 8GB