1D Heat Equation
1次元熱伝導方程式を数値計算で解く 〜偏微分方程式入門〜
はじめに
「熱い鉄の棒の端を加熱し続けたら、温度はどう伝わっていくか?」
このような熱の伝わり方を知りたいとき、物理学では熱伝導方程式という偏微分方程式が登場します。
一見すると難解な記号の羅列に見えますが、これをコンピュータで扱える形(差分方程式)に変換すると、実は「自分の温度は、両隣の温度で決まる」という、非常にシンプルな足し算と引き算の世界が見えてきます。
本記事では、この熱伝導方程式を「差分化」する過程を詳しく解説し、実際に数値がどのように変化していくかを見ていきます。
偏微分方程式から差分方程式へ(導出プロセス)
コンピュータは「無限に小さい変化(微分)」を直接扱うことができません。そこで、時間と空間を細かいメッシュ(格子)に区切り、微分を「ごく短い区間の引き算」に近似します。これを差分化と呼びます。
2.1 空間と時間の分割(離散化)
まず、計算したい世界をグリッド状に分割します。
- 空間 ($x$) : 棒を $\Delta x$ 間隔で区切ります。位置をインデックス $i$ で表します。($x_i = i \cdot \Delta x$)
- 時間 ($t$) : 時間を $\Delta t$ 刻みで進めます。時刻をインデックス $n$ で表します。($t_n = n \cdot \Delta t$)
ここでの目標は、「今の時刻 ($n$) のデータを使って、次の時刻 ($n+1$) の温度 $u_i^{n+1}$ を求める式」を作ることです。
2.2 時間の変化(左辺の変形)
左辺 $\frac{\partial u}{\partial t}$ は、「時間の変化に対する温度の変化率」です。これは単純に、「未来の値」から「今の値」を引いて、時間刻みで割ることで近似できます。
2.3 空間の曲がり具合(右辺の変形)
右辺 $\frac{\partial^2 u}{\partial x^2}$ は、「位置による変化率(傾き)」の、さらに「変化率」を表す 2階微分 です。
これは、(右隣との傾き) - (左隣との傾き) を距離 $\Delta x$ で割ることで求められます。
ステップA:傾き(1階微分)を求める
自分(位置 $i$)を中心にして、右側の傾きと左側の傾きをそれぞれ求めます。
- 右隣との傾き: $\frac{u_{i+1} - u_i}{\Delta x}$
- 左隣との傾き: $\frac{u_i - u_{i-1}}{\Delta x}$
ステップB:傾きの変化(2階微分)を求める
2階微分は、この「右の傾き」と「左の傾き」の差を取って、さらに距離 $\Delta x$ で割ったものです。
これを整理すると、非常にシンプルな形になります。
2.4 式の合体と完成
左辺と右辺をイコールで結びます。
私たちが知りたいのは「未来の値 ($u_i^{n+1}$」だけなので、これについて解きます(左辺に残して他を右辺へ移項)。すると、プログラムで記述できる差分方程式が完成します。
ただし係数 $r = \frac{\alpha \Delta t}{(\Delta x)^2}$
計算の意味と数値シミュレーション
導出した式 $u_{\text{new}} = u_{\text{current}} + r \times (u_{\text{left}} - 2u_{\text{current}} + u_{\text{right}})$ の意味を考えてみましょう。
括弧の中身は、変形すると $(u_{\text{left}} + u_{\text{right}}) - 2u_{\text{current}}$ とも見れます。これは「両隣の合計」と「自分の2倍」の差を見ています。
- もし「両隣の平均」より自分が低ければ $\rightarrow$ プラスになり、温度が上がる。
- もし「両隣の平均」より自分が熱ければ $\rightarrow$ マイナスになり、温度が下がる。
つまり、「両隣と馴染むように温度が変わっていく」という拡散現象を数学的に表しているのです。
【図解】差分化のイメージ:3点間の相互作用
「自分 ($u_i$)」の次の温度は、
左右の「隣 ($u_{i-1}, u_{i+1}$)」との温度差によって決まる。
手計算による数値追跡例
実際に簡単な数字を入れて、熱が伝わる様子を追ってみましょう。
(係数 $r = 0.5$、左端は常に100固定、初期値は0)
t=1 (1step後):
2番目の点: 0 + 0.5 * (100 - 0 + 0) = 50
結果: [ 100, 50, 0, 0, 0 ]
t=2 (2step後):
2番目の点: 50 + 0.5 * (100 - 100 + 0) = 50
3番目の点: 0 + 0.5 * (50 - 0 + 0) = 25
結果: [ 100, 50, 25, 0, 0 ]
このように、単純な計算を繰り返すだけで、熱が左から右へと徐々に伝わり、グラデーションが形成されていく様子が計算できます。
結果
導出した差分方程式を解析した結果を示します。 今回は直接プログラミング言語でループ処理を書くのではなく、回路シミュレータSPICEに偏微分方程式を解かせる「SPICE指向型解析法」を用いました。
SPICEでの実装(半離散化 / Method of Lines)
SPICEのB電源で記述したのは、前節までの差分式とは異なり、空間だけバラバラ(離散化)にして、時間は連続のまま(微分)にした式です。
これは「変化のスピード(電流)を与える式」であるため、ここに時間刻み $\Delta t$ は含まれません。SPICE内部のコンデンサが連続時間での積分を担います。
ここでの係数(SPICEパラメータのCOEFF)は $\frac{\alpha}{(\Delta x)^2}$ となります。($\Delta t$ がないことに注意!)
なお、本計算では 空間メッシュ数 N=5 としました。
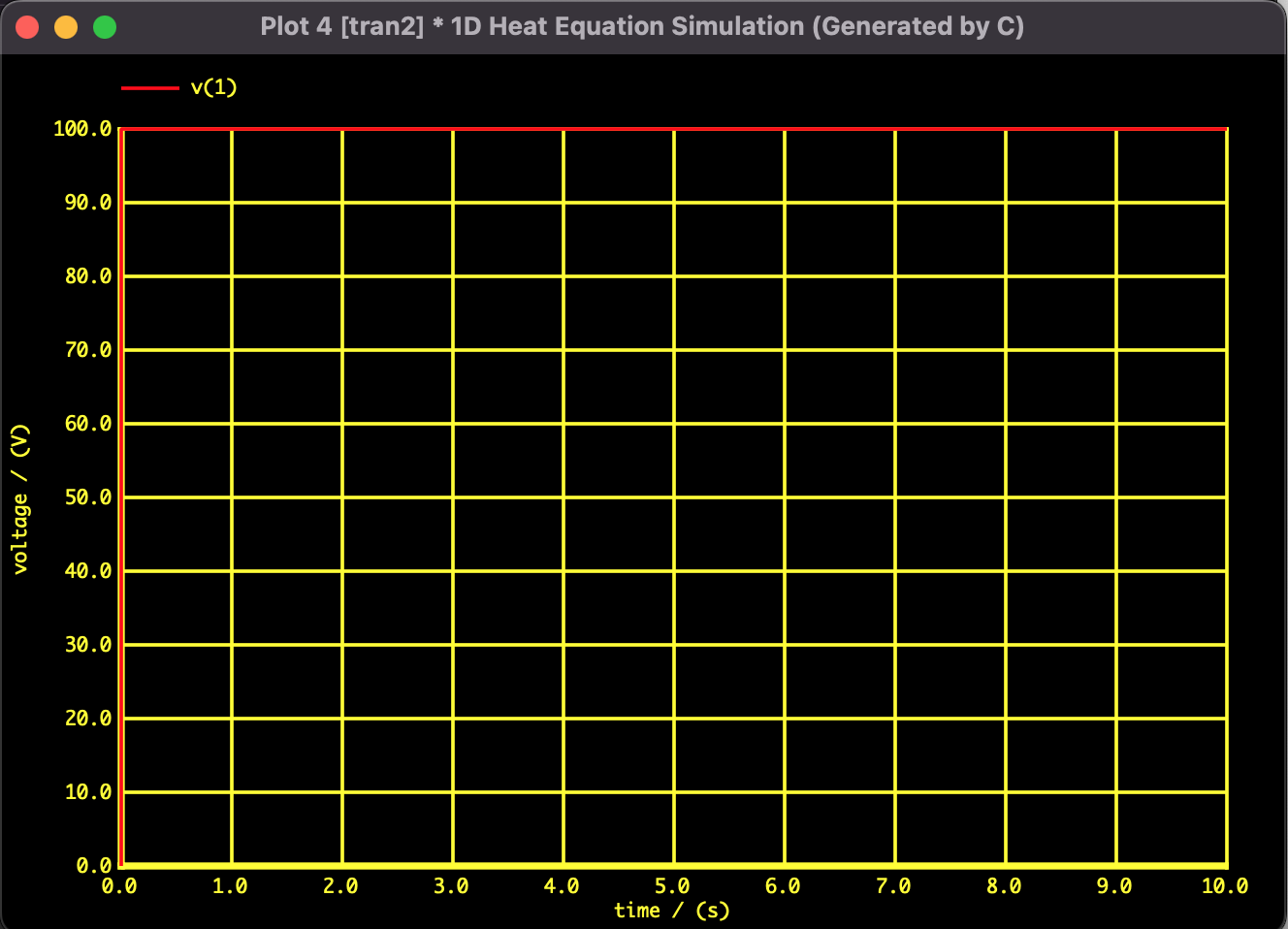
図1:温度分布の時間変化。左端(Node 1)が100V(℃)に固定されており、時間の経過(ステップごと)とともに熱が右側へ拡散し、最終的に直線的な温度勾配(定常状態)へ収束していく様子が確認できる。
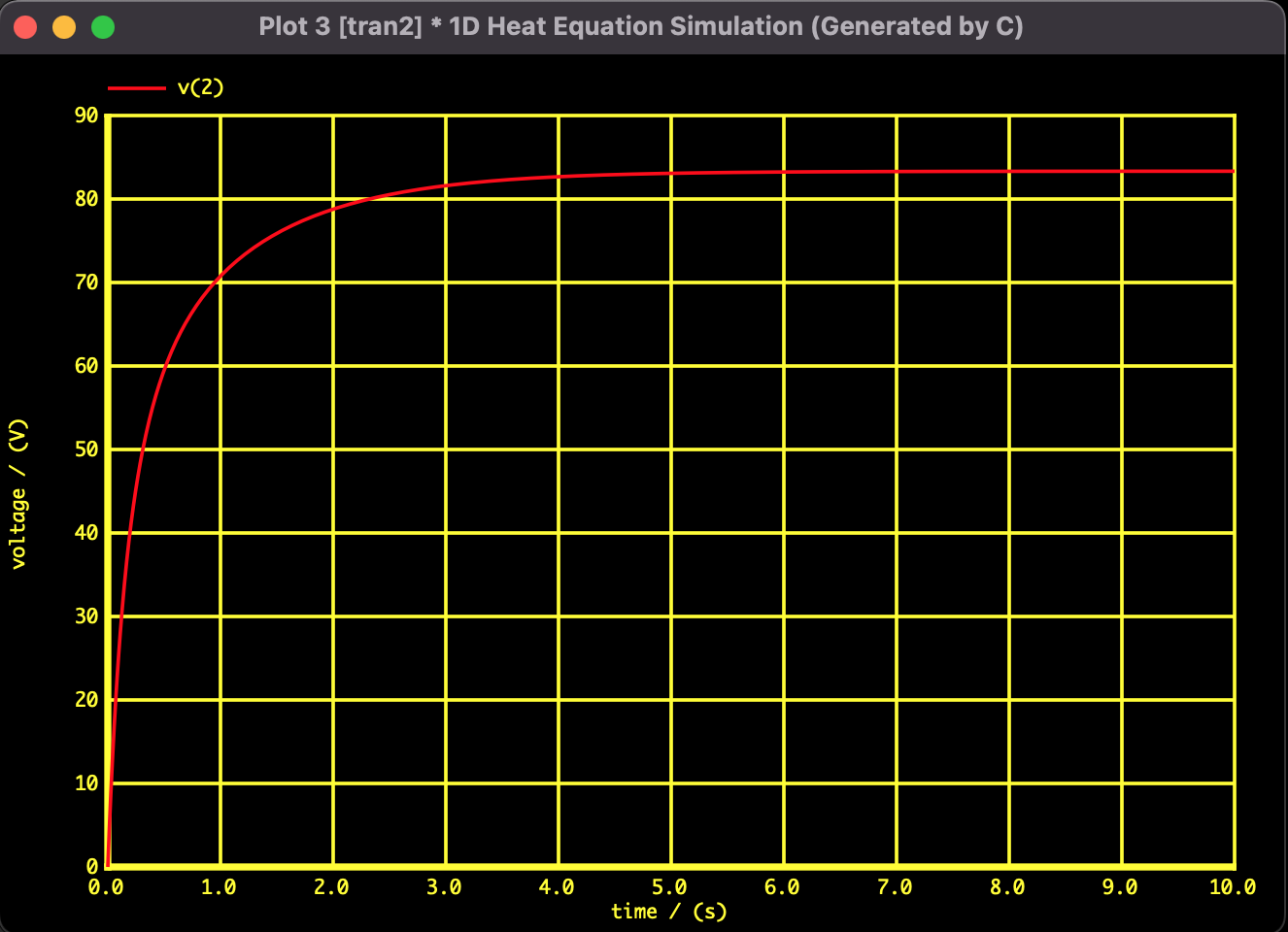
図2:特定ノード(Node 2:左端から1つ目の分割点)の過渡応答。$t=0$ での急激な立ち上がりから、一次遅れ系のように約83.3V(理論値)へ収束している。発散することなく安定して解けていることがわかる。
解析環境
- SPICE: Mac SPICE3
- PC: MacBook
- OS: macOS Monterey 12.7.6
- CPU: 1.2GHz デュアルコア Intel Core m5
- メモリ: 8GB
この規模の計算では現在のPC環境であれば一瞬で収束するため、詳細な計算時間の計測は割愛いたします。