Linear Complementarity Problem
線形相補性問題
1. 線形相補性問題(LCP)とは
物理シミュレーションの衝突判定(剛体は互いにめり込まない)や、経済学の市場均衡などで現れる、以下の条件を満たすベクトル $w, z$ を求める問題を線形相補性問題(LCP)と呼びます。
最後の「相補性条件 ($w^T z = 0$)」と「非負条件」の組み合わせは、要素ごとに見れば「$w_i$ と $z_i$ の少なくとも片方は必ず $0$ でなければならず、かつ両方ともマイナスになってはいけない」という、一種のスイッチング動作を意味します。
2. 一般的な解法と今回のアプローチ
LCPは古くから研究されており、解くための専用アルゴリズムがいくつか確立されています。
- ピボット法(レムケ法など): 単体法のように変数を入れ替えながら解を探す手法。
- 内点法: 実行可能領域の内部を通って最適解に収束させる手法。
しかし今回は、これらの専用ソルバーを使わず、より汎用的な「ニュートン法」や「ホモトピー法」を用いて解くことに挑戦します。
そのためには、不等式($\ge 0$)を含むこの問題を、これら強力なソルバーが扱える「非線形方程式($=0$)」の形に帰着させる必要があります。
3. 非線形方程式への帰着:NCP関数
「非負かつ相補的($a \ge 0, b \ge 0, ab=0$)」という条件を、一本の等式 $\phi(a, b) = 0$ で表現できる関数のことをNCP関数と呼びます。
代表的な2つのNCP関数を紹介します。
A. Min関数(絶対値の利用)
最も直感的なのは、「小さい方が0であればよい」という考え方です。
どちらかが負なら $\min$ は負になり、両方正なら $\min$ は正になります。「片方が0、もう片方が正(または0)」の時だけ0になるため、LCPの条件と等価です。
特徴: 直感的ですが、絶対値を含むため $a=b$ のラインでグラフが折れ曲がり(微分不可能)、ニュートン法の収束が悪くなる欠点があります。
B. Fischer-Burmeister関数(今回の主役)
そこで、絶対値の代わりに滑らかな曲線を持つFischer-Burmeister(フィッシャー・ブルマイスター)関数を採用します。
なぜ置き換えられるのか?(等価性の証明)
式を変形して2乗してみます。
$\sqrt{a^2 + b^2} = a + b$
$\implies (a^2 + b^2) = (a + b)^2 = a^2 + 2ab + b^2$
$\implies 0 = 2ab \iff ab = 0$
これにより「積が0(少なくとも片方は0)」が導かれます。また、元の式の左辺(ルート)は非負なので、右辺 $a+b$ も非負でなければならず、積が0という条件と合わせると必然的に $a, b \ge 0$ となります。
特徴: 原点以外で滑らか(微分可能)であり、ニュートン法との相性が非常に良いため、今回はこちらを使用します。
4. 方程式の定式化
上記のFB関数 $\phi_{FB}$ を、ベクトルの各要素 $(w_i, z_i)$ に適用します。
さらに、$w = Mz + q$ の関係式を代入して $w$ を消去すれば、$z$ だけの未知数を持つ連立非線形方程式を作ることができます。
これで、LCPは単なる「$F(z)=0$ を解く問題」に帰着されました。
5. 解析結果
シンプルな2次元の例題として、以下のパラメータを設定しました。
この場合、線形関係式 $w = Mz + q$ は $w_i = -z_i + 1$、つまり $w = 1 - z$ となります。
これを Fischer-Burmeister 関数 $\phi_{FB}(w, z) = \sqrt{w^2 + z^2} - (w + z) = 0$ に代入すると、実際に解くべき方程式は以下のようになります。
※ $(1-z_i) + z_i = 1$ となるため、式が非常にシンプルになります。
この方程式には、以下の4つの解が存在します。
ニュートン法とホモトピー法で、これら全てを発見できるかを検証します。なお、今回はSPICE指向型解析法で解析を行いました。
- ① $z = (0, 0)^T$
- ② $z = (1, 1)^T$
- ③ $z = (0, 1)^T$
- ④ $z = (1, 0)^T$
結果 1:ニュートン法による収束
初期値を変えてニュートン法を適用した際の収束の様子です。
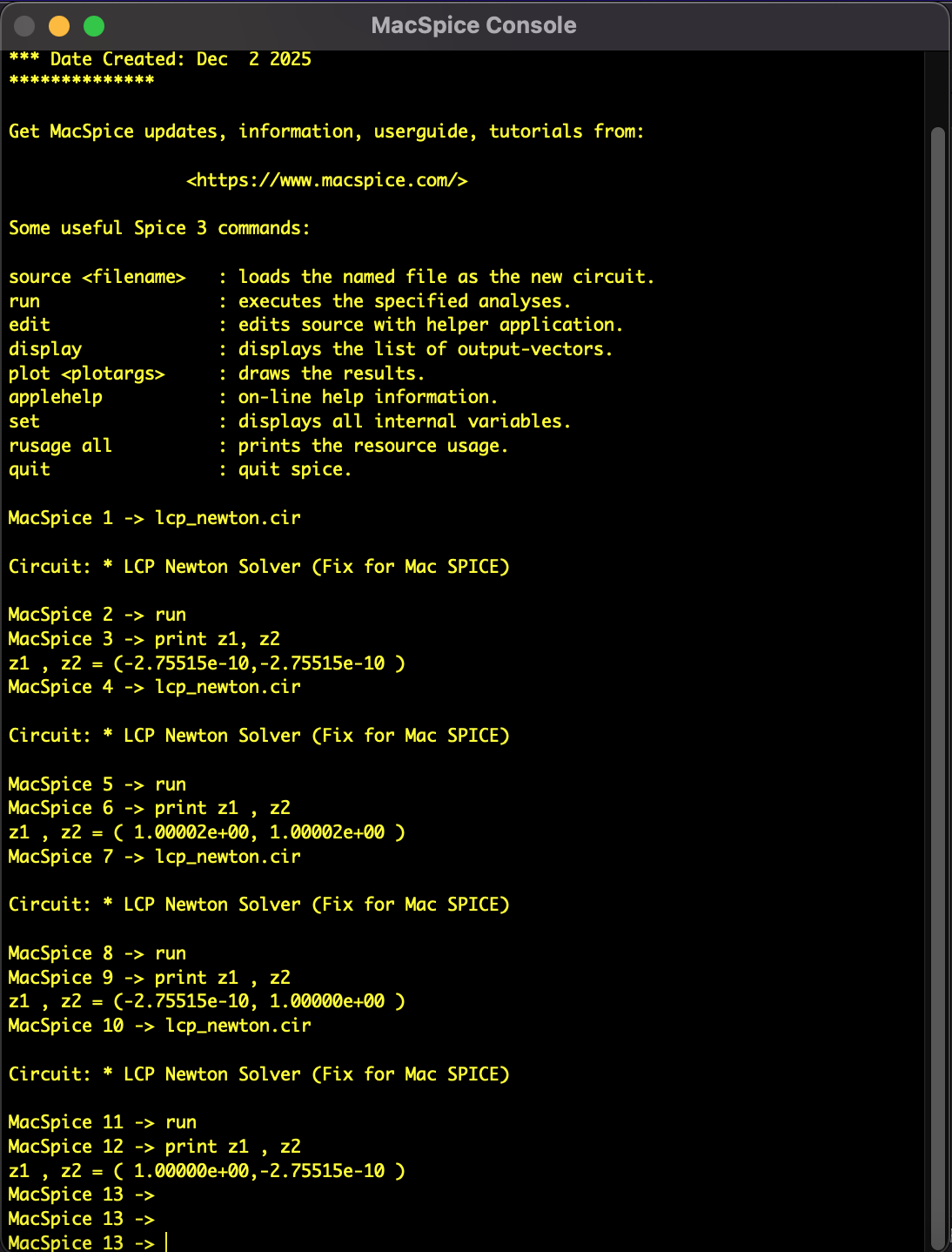
図1:ニュートン法の収束結果
結果 2:ホモトピー法による解の探索
ニュートンホモトピー法を用いて、パラメータ変化に伴う解の軌跡を追跡した結果です。初期値を帰れば別の解に収束し全部の解を見つけられますが、一回の解析で全解を求めることはできませんでした。
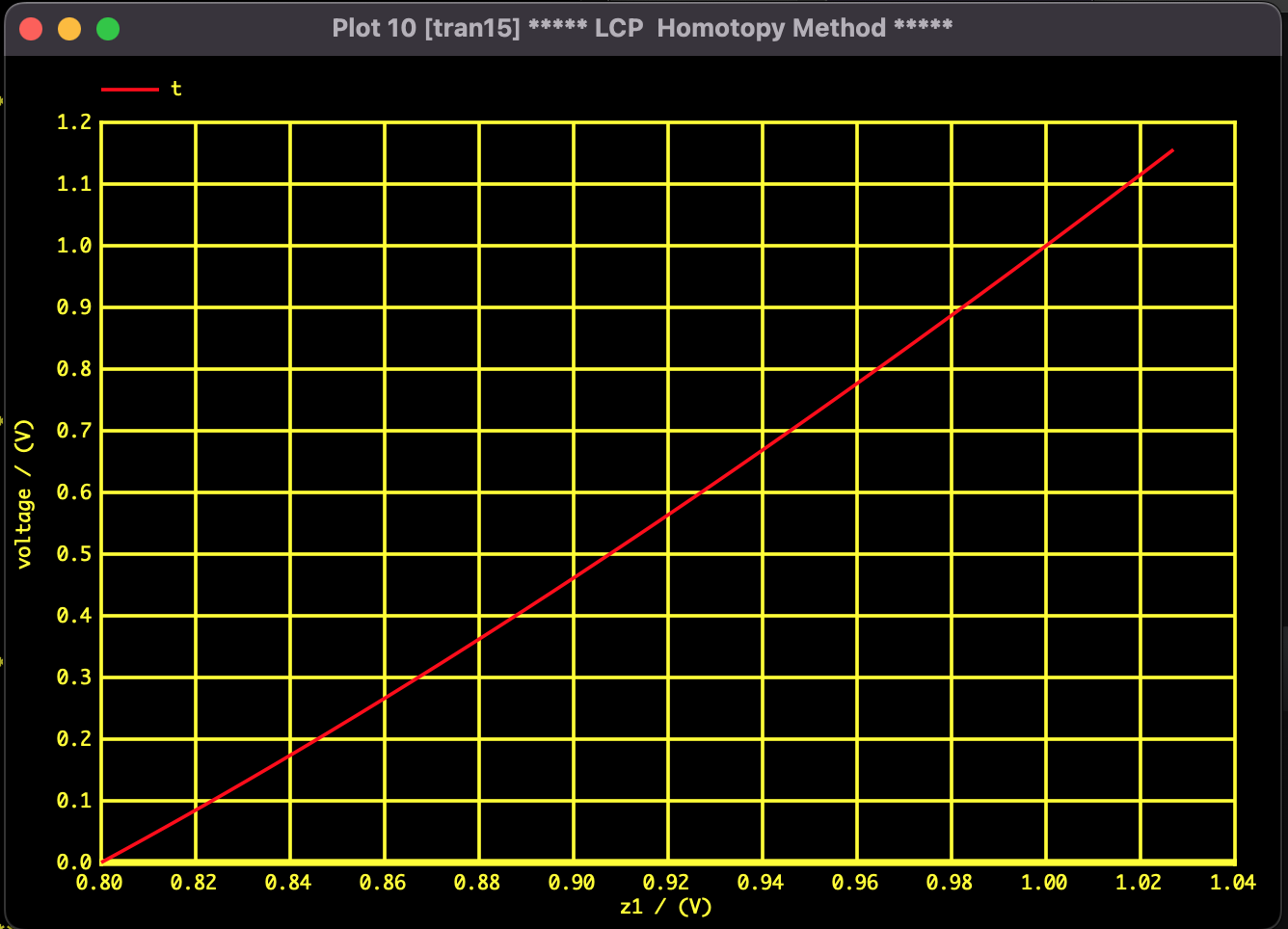
図2:ホモトピーパスの軌跡($z_1$)
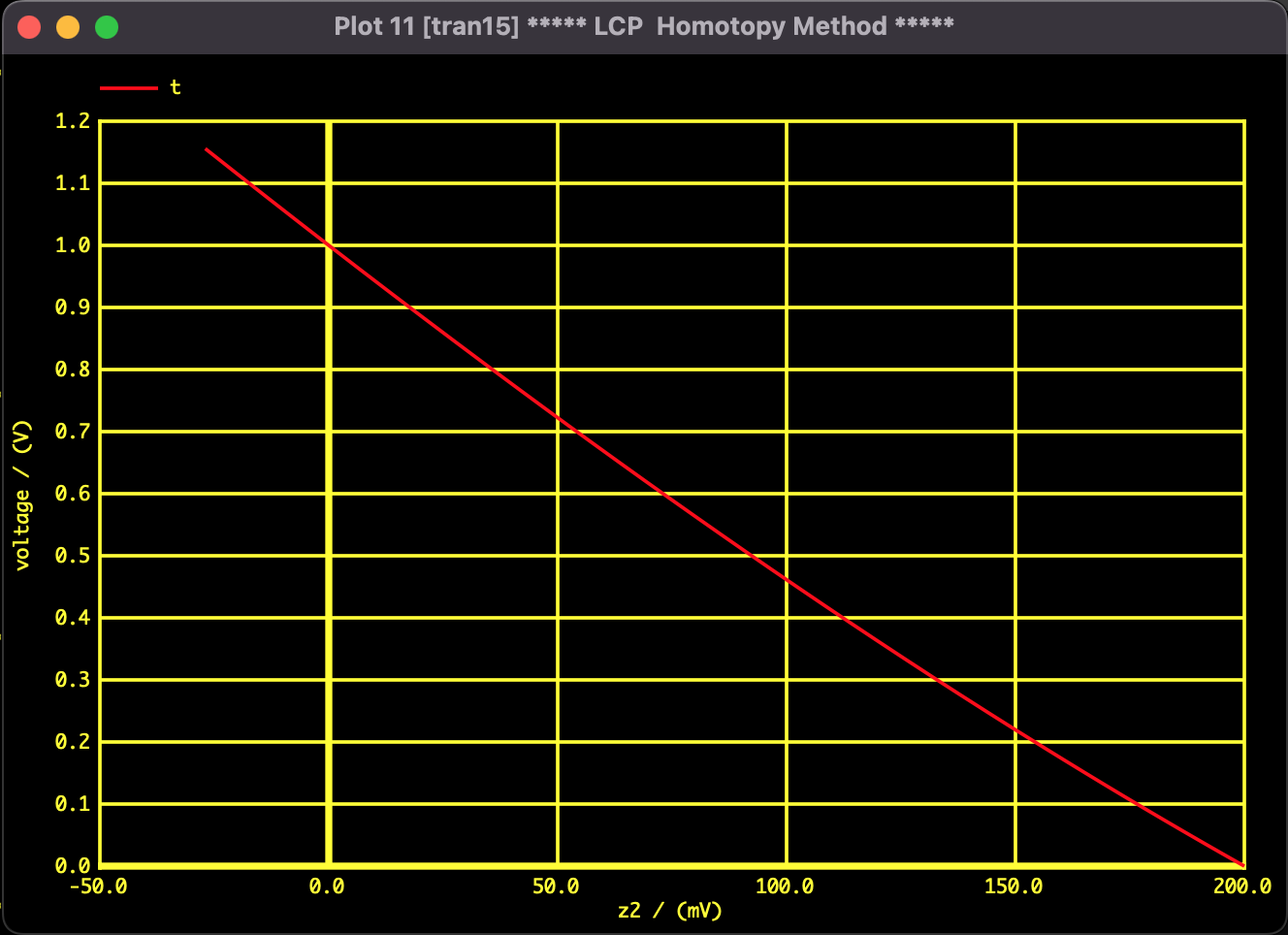
図3:ホモトピーパスの軌跡($z_2$)