Linear Programming

線形計画問題 (Klee-Minty Problem)

1. 線形計画問題とは

線形計画問題（Linear Programming, LP）は、一次不等式または等式の制約条件下で、線形の目的関数を最大化（または最小化）する最適化問題です。

一般的には以下のような標準形で定式化されます。

\[ \begin{aligned} \text{Minimize} \quad & \boldsymbol{c}^T \boldsymbol{x} \\ \text{subject to} \quad & A\boldsymbol{x} = \boldsymbol{b} \\ & \boldsymbol{x} \ge 0 \end{aligned} \]

ここで、$\boldsymbol{x}$ は決定変数ベクトル、$A$ は係数行列、$\boldsymbol{b}$ は制約ベクトル、$\boldsymbol{c}$ はコストベクトルを表します。

通常は単体法（Simplex Method）や内点法を用いて解かれますが、本研究ではこれを力学系（エネルギー最小化プロセス）と捉え、連続的な数値解析手法を用いて解の探索を行いました。

2. Klee-Minty問題

解析対象として、KleeとMintyによって1972年に提案された「Klee-Minty問題」を取り上げます。

この問題は、超立方体が歪んだような実行可能領域を持ち、単体法におけるピボット選択を最悪のケース（指数関数時間）に陥らせるベンチマークとして知られています。その形状は極めて複雑で、多くの局所的な罠や、曲がりくねった稜線を持っています。

$N$ 変数の場合、以下のように定式化されます。

\[ \begin{aligned} \text{Maximize} \quad & \sum_{j=1}^{N} 10^{N-j} x_j \\ \text{subject to} \quad & 2 \sum_{j=1}^{i-1} 10^{i-j} x_j + x_i \le 100^{i-1} \quad (i=1, \dots, N) \\ & x_j \ge 0 \end{aligned} \]

係数に $10$ のべき乗が含まれるため、変数のスケールが極端に異なり、数値計算的にも非常に「悪条件（Ill-conditioned）」な問題となります。

3. 拡大ラグランジュ乗数法（凸定式化）

不等式制約 $g_i(\boldsymbol{x}) \le 0$ を扱う手法として、大きく分けて二つのアプローチがあります。

(A) スラック変数を用いた等式化（非凸化のリスク）

教科書的な手法として、スラック変数 $y_i$ を導入し、不等式を等式 $g_i(\boldsymbol{x}) + y_i^2 = 0$ に変換してから拡張ラグランジュ関数を構成する方法があります。

\[ L(\boldsymbol{x}, \boldsymbol{y}, \boldsymbol{\lambda}) = f(\boldsymbol{x}) + \sum \lambda_i (g_i(\boldsymbol{x}) + y_i^2) + \frac{\rho}{2} \sum (g_i(\boldsymbol{x}) + y_i^2)^2 \]

しかし、この手法は $y_i^2$ の項を含むため、元の問題が凸（Convex）であっても、エネルギー関数全体は非凸（Non-convex）になってしまいます。その結果、Klee-Minty問題のような複雑な地形では局所解（Local Minima）に陥りやすく、正解にたどり着けないことが確認されました。

(B) Rockafellarによる不等式定式化（凸性の維持）

そこで本解析では、スラック変数を用いず、不等式制約を直接扱うRockafellarの定式化（式 1.30）を採用しました。この手法は、制約違反時のみペナルティを与える「片側だけのバネ」のようなポテンシャルを形成し、凸性を維持したまま大域的最適解へ収束させることができます。

[基本式]

\[ L(\boldsymbol{x}, \boldsymbol{\lambda}, \kappa) = f(\boldsymbol{x}) + \frac{\kappa}{2} \sum \left( [g_i(\boldsymbol{x})]_{-} \right)^2 + \sum \lambda_i [g_i(\boldsymbol{x})]_{-} \]

定義：$[g_i(\boldsymbol{x})]_{-} = \min \{ -\frac{\lambda_i}{\kappa}, \ g_i(\boldsymbol{x}) \}$

上記の式は、平方完成による式変形を経て、以下のような実装に適したシンプルな形（ReLUのような整流作用を持つ式）に帰着されます。

[実装式]

\[ L \approx f(\boldsymbol{x}) + \frac{1}{2\kappa} \sum \left[ \min \left( 0, \ \kappa g_i(\boldsymbol{x}) + \lambda_i \right) \right]^2 \]

4. 線形計画問題の非線形方程式化 (KKT条件)

最適化問題を解くもう一つのアプローチとして、最適性の必要十分条件であるKKT条件（Karush-Kuhn-Tucker条件）を立式し、これを連立非線形方程式として解く手法を用いました。

線形計画問題のKKT条件は、主問題と双対問題の関係から以下のように導出されます。

主問題と双対問題からの導出

まず、主問題 (Primal Problem) と、それに対応する双対問題 (Dual Problem) を考えます。

主問題 (P): $\text{Min } \boldsymbol{c}^T \boldsymbol{x} \quad \text{s.t. } A\boldsymbol{x}=\boldsymbol{b}, \ \boldsymbol{x} \ge 0$

双対問題 (D): $\text{Max } \boldsymbol{b}^T \boldsymbol{y} \quad \text{s.t. } A^T \boldsymbol{y} + \boldsymbol{s} = \boldsymbol{c}, \ \boldsymbol{s} \ge 0$

最適解においては、主問題と双対問題の双方で制約条件が満たされている必要があります（実行可能性）。

主実行可能条件： $A\boldsymbol{x} = \boldsymbol{b}, \ \boldsymbol{x} \ge 0$
双対実行可能条件： $A^T \boldsymbol{y} + \boldsymbol{s} = \boldsymbol{c}, \ \boldsymbol{s} \ge 0$

さらに、強双対定理 (Strong Duality Theorem) により、最適解では主問題の最小値と双対問題の最大値が一致します（Duality Gap = 0）。

$\boldsymbol{c}^T \boldsymbol{x} = \boldsymbol{b}^T \boldsymbol{y}$

ここで、$A\boldsymbol{x}=\boldsymbol{b}$ および $\boldsymbol{c} = A^T \boldsymbol{y} + \boldsymbol{s}$ を代入して整理すると、以下の関係が得られます。

$(A^T \boldsymbol{y} + \boldsymbol{s})^T \boldsymbol{x} = (A\boldsymbol{x})^T \boldsymbol{y} \iff \boldsymbol{y}^T A \boldsymbol{x} + \boldsymbol{s}^T \boldsymbol{x} = \boldsymbol{y}^T A \boldsymbol{x}$
$\therefore \boldsymbol{s}^T \boldsymbol{x} = 0$

$\boldsymbol{x} \ge 0, \boldsymbol{s} \ge 0$ であるため、内積がゼロになるには、各成分ごとに $x_i s_i = 0$ でなければなりません。これを相補性条件 (Complementarity Condition) と呼びます。

以上の3つの条件（主制約、双対制約、相補性）をまとめたものが、今回解くべき連立方程式（KKTシステム）です。

\[ \begin{aligned} Ax &= b \\ A^T y + s &= c \\ X s &= 0 \quad (\text{または } X s = \mu) \\ (x, s) &\ge 0 \end{aligned} \]

5. 解析結果

本解析では $N=3$ の場合のKlee-Minty問題を扱いました。数値計算結果を検証するための、数学的な理論解（正解）は以下の通りです。

Variable	Exact Solution ($N=3$)
$x_1$	0
$x_2$	0
$x_3$	10,000
Objective Value	10,000

① 拡大ラグランジュ乗数法の結果

凸定式化を用いた解析結果です。SPICE指向型解析法を用いて解析を行いました。目的関数値が時間とともに単調に減少し、理論的な最適解へ滑らかに収束していることが確認できます。

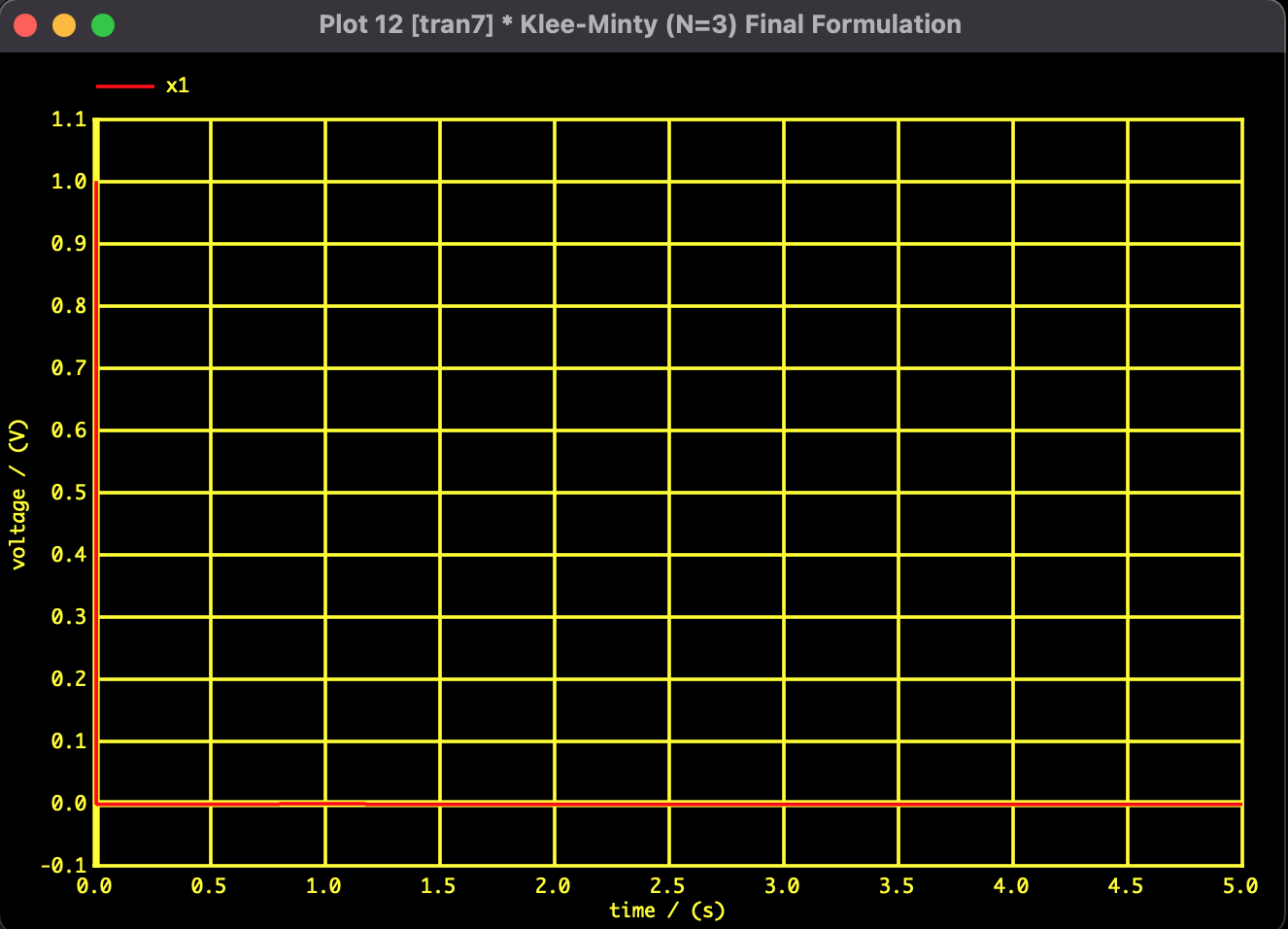
Heat Equation Result - Spatial Distribution

図1：$x_1$の収束推移

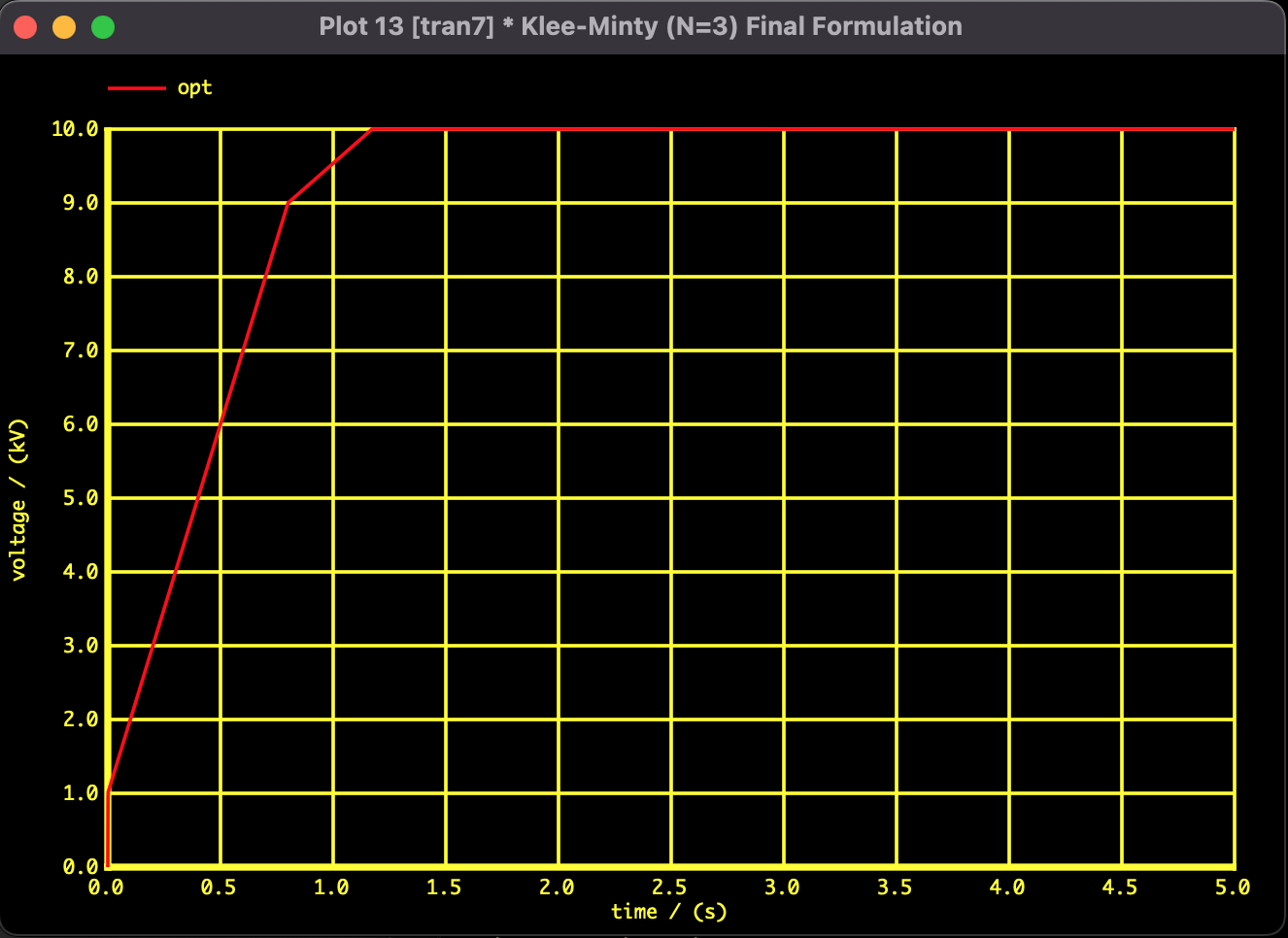
図2：目的関数値の収束推移

② ニュートン法の結果

線形計画問題を非線形方程式にし、修正ニュートン法を適用しました。SPICE指向型解析法を用いて解析を行いました。しかし、解は収束しませんでした。

初期値からの直線探索において、Klee-Minty問題特有の制約条件の壁（$x \ge 0$）を飛び越えて負の領域に突入してしまい、不適解で停止しました。

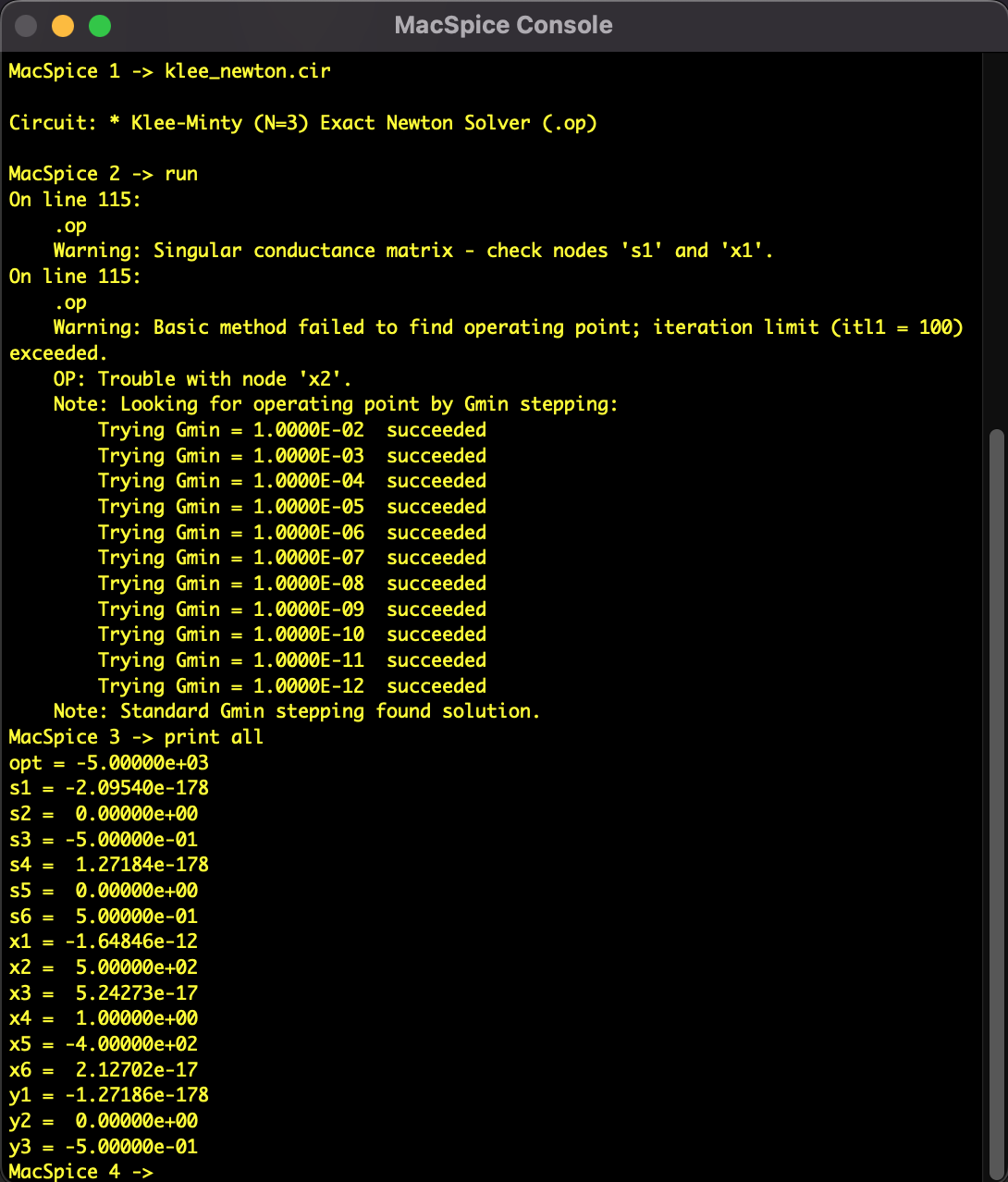
図3：ニュートン法の解析結果

③ ホモトピー法の結果

ニュートン法での失敗を受け、パラメータ $t$ を導入して方程式を連続的に変形させるホモトピー法（Homotopy Method）を適用しました。

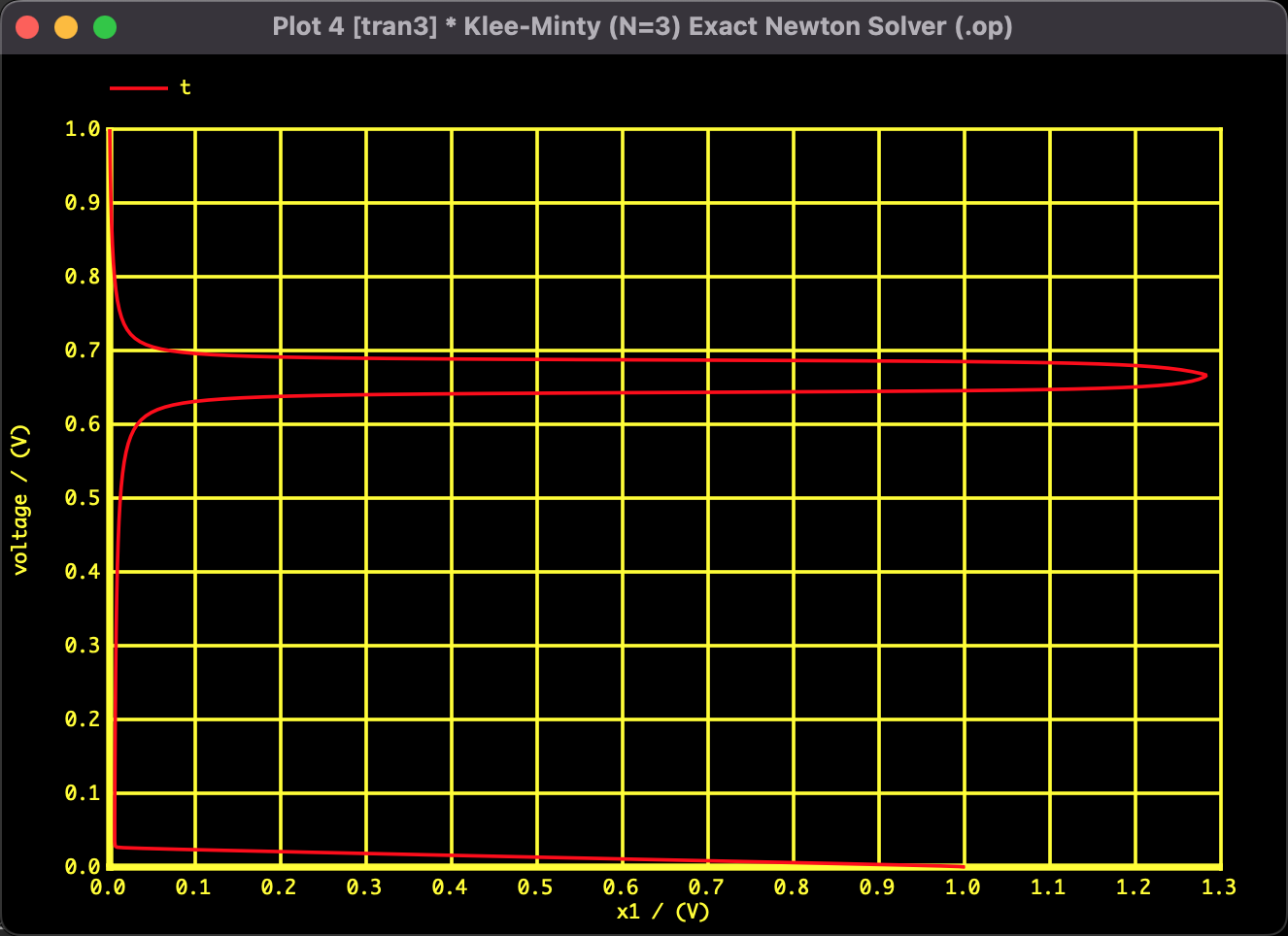
図4：$x_1$の収束推移

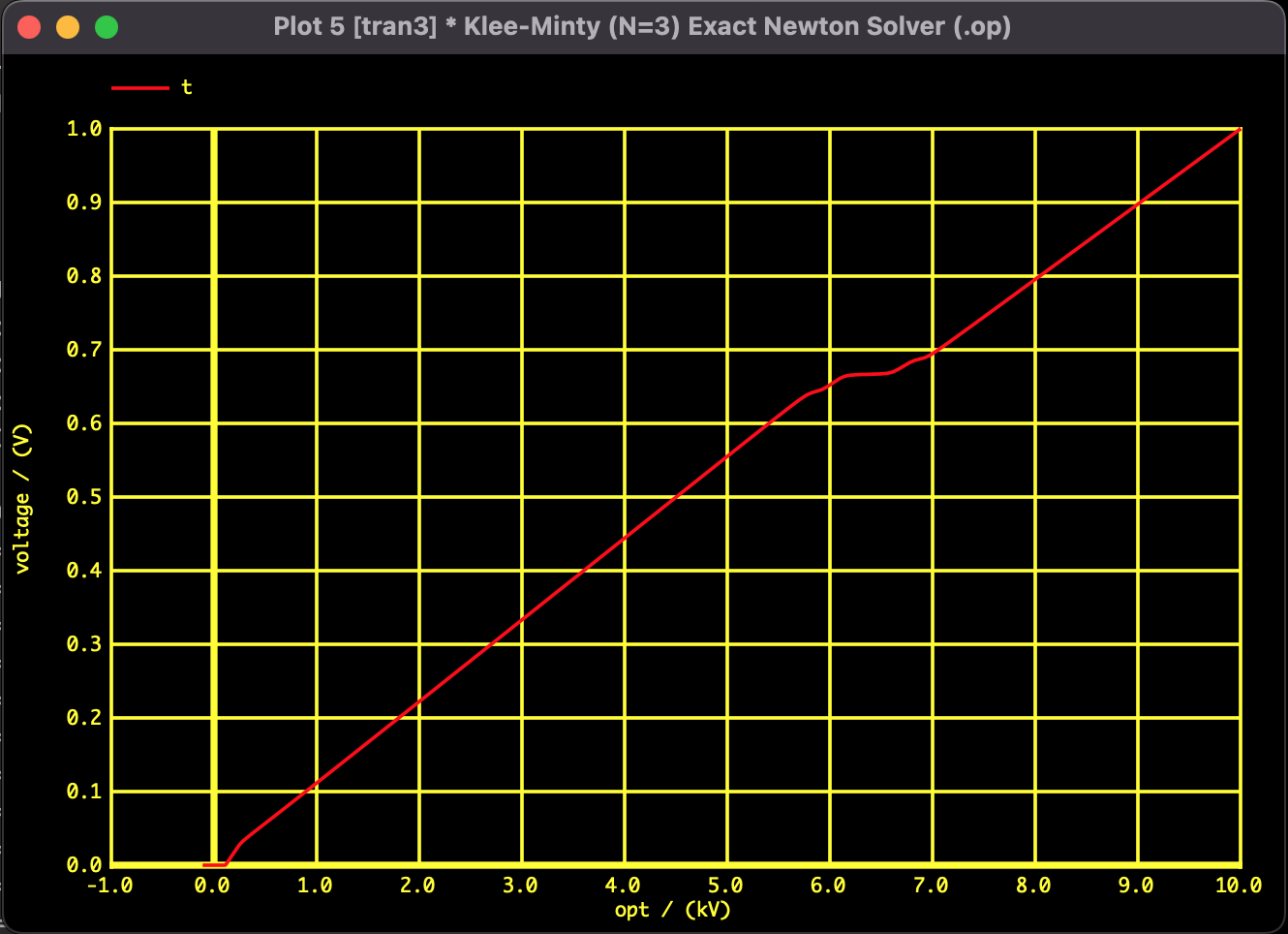
図5：目的関数値の収束推移

$x_1$ の軌跡は単純な直線ではなく、大きく蛇行する「S字カーブ」を描いています。これは、ソルバーが制約条件の壁に衝突しそうになるたびに、ギリギリで壁を回避しながら最適解へのルートを探っている様子を表しています。

解析環境

SPICE： Mac SPICE3
PC： MacBook
OS： macOS Monterey 12.7.6
CPU： 1.2GHz デュアルコア Intel Core m5
メモリ： 8GB

この規模の計算では現在のPC環境であれば一瞬で収束するため、詳細な計算時間の計測は割愛いたします。