JP / EN

Rosenbrock Function

1. ローゼンブロック関数

\[ f_1(\boldsymbol{x}) = 10(x_2 - x_1^2) = 0 \] \[ f_2(\boldsymbol{x}) = 1 - x_1 = 0 \]

特徴

数値最適化のベンチマークとして最も有名ですが、その勾配ベクトルをゼロとおくことで、非線形代数方程式のテストケースとして非常によく使われます。

解 $(1, 1)$ は非常に細長く曲がった「谷」の底にあります。アルゴリズムが解に近づく際、収束速度が極端に遅くなる傾向があるため、収束性能の評価に最適です。

解の挙動（可視化）

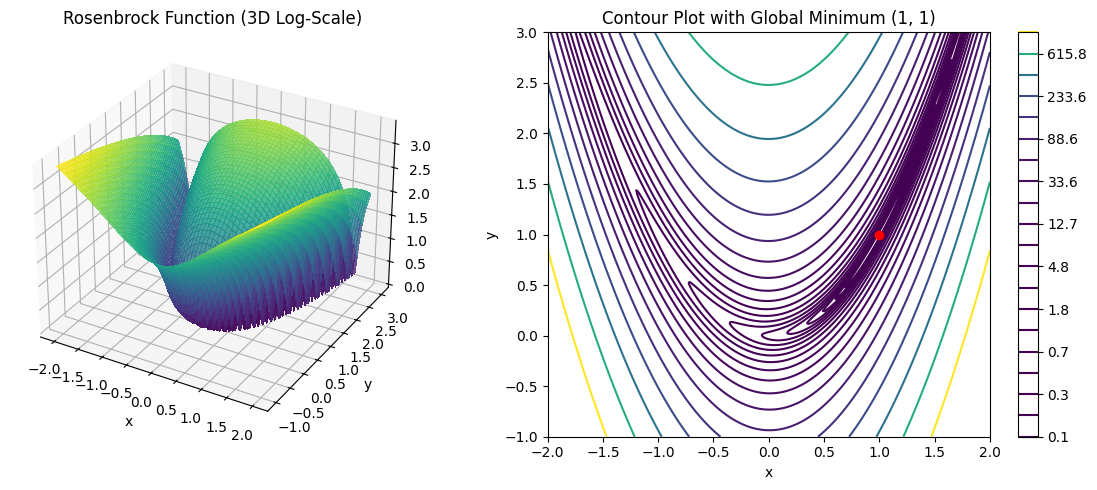
Rosenbrock Visualization

図1：ローゼンブロック関数の3Dサーフェスプロット。解(1,1)に向かって非常に細長い谷が形成されていることがわかる。

結果

ローゼンブロック関数をニュートン法で解いた結果を示します。

今回は直接プログラミングするのではなく、式を回路で記述して回路シミュレーターSPICEで解くという逆転的発想に基づいた方法論である「SPICE指向型解析法」を用いて解析を行いました。

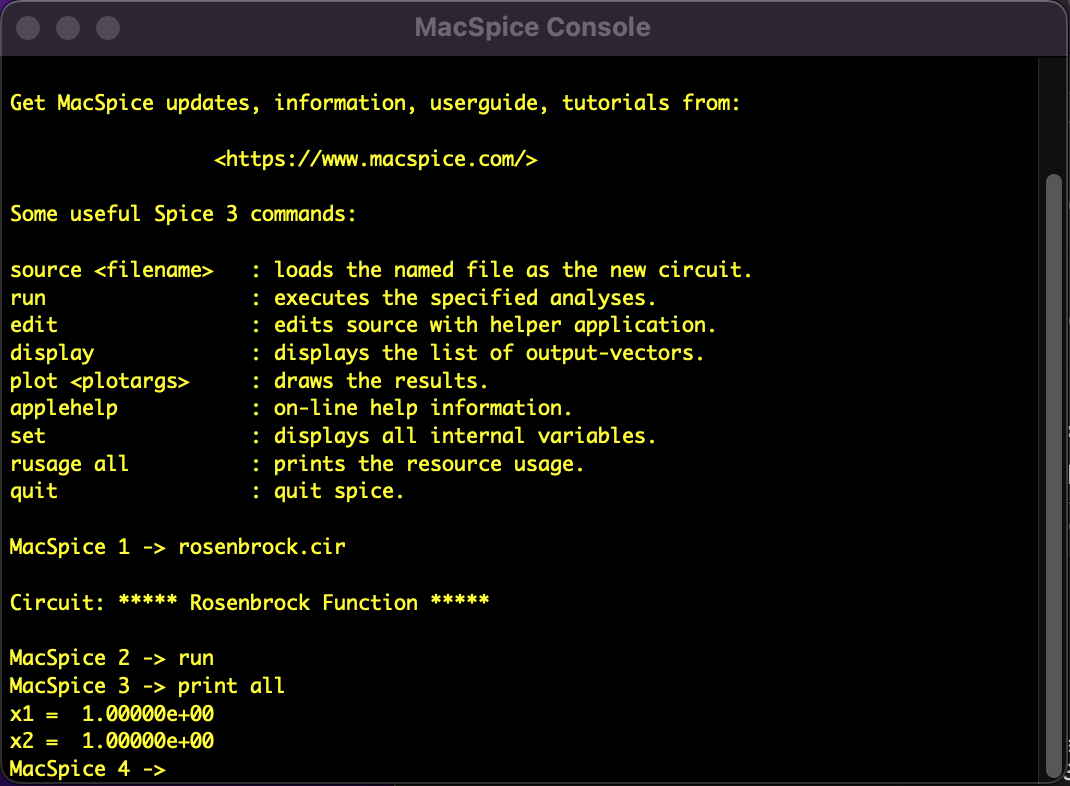
SPICE Analysis Result

図2：SPICE指向型解析法によるローゼンブロック関数の解析結果

解析環境

  • SPICE： Mac SPICE3
  • PC： MacBook
  • OS： macOS Monterey 12.7.6
  • CPU： 1.2GHz デュアルコア Intel Core m5
  • メモリ： 8GB

この規模の計算では現在のPC環境であれば一瞬で収束するため、詳細な計算時間の計測は割愛いたします。