Homotopy Global Search
ホモトピー法による全解探索への挑戦
闇夜のカラスを一羽見つけることは容易でも、そこにいる全てのカラスを見つけることは至難の業である。
非線形方程式における「全解探索」という難問について。
1. 「すべての解」を見つけるという難問
非線形代数方程式 $f(x)=0$ を解く際、我々は通常、ニュートン法などの反復解法を用います。 しかし、これらの方程式は初期値に依存し、最も近い解(局所解)に収束した時点で計算を終了してしまいます。
実社会の問題、たとえば化学平衡やロボットの逆運動学などにおいては、「解が一つ見つかれば良い」とは限りません。 物理的に意味のある解を見逃さないためには、その空間に存在する「すべての解」を網羅的に探し出す必要がありますが、これは数学的に非常に困難な課題とされています。
2. 1972年の挑戦状:Braninのベンチマーク
全解探索のアルゴリズムを検証するためのベンチマーク問題は数多く存在しますが、その中でも特に興味深いのが、F. H. Branin博士が1972年の論文で提示した問題です。
F. H. Branin, "Widely Convergent Method for Finding Multiple Solutions of Simultaneous Nonlinear Equations", IBM J. Res. Dev., 1972.
この論文で扱われているのは、通称「Six-Hump Camel Function(6こぶラクダ関数)」と呼ばれる関数の勾配系方程式です。
この問題の難しさは、解の個数と配置にあります。 極小値、極大値、そして不安定な鞍点(Saddle Points)を合わせると、解の総数は実に15個。 これらが複雑に入り組んだ地形の中に点在しており、単純な探索では一部の解しか見つけることができません。
3. ニュートン・ホモトピー法によるアプローチ
この15個の解を一網打尽にするために、今回は「ニュートン・ホモトピー法(Newton-Homotopy Method)」を採用しました。
ホモトピー法とは、いきなり難しい問題 $f(x)=0$ を解くのではなく、答えが分かっている簡単な問題 $f(x_0)=0$ からスタートし、それを連続的に変形(Deform)させながら解の軌道を追跡する手法です。
$t$: Homotopy parameter ($0 \to 1$)
パラメータ $t$ を $0$ から $1$ へと変化させることで、解の曲線(パス)が空間内に描かれます。 Branin博士の手法(行列式の符号反転法)を組み合わせることで、一つの解から次の解へと、まるで数珠つなぎのように15個すべての解を巡る一本の軌跡を描くことが可能になります。
4. 実験結果:15個の解を巡る旅
以下に、SPICE指向型解析法を用いて探索を行った結果を示します。 一度の探索で、理論値通り15個すべての解を発見し、Branin博士の論文にある軌跡を完全に再現することに成功しました。
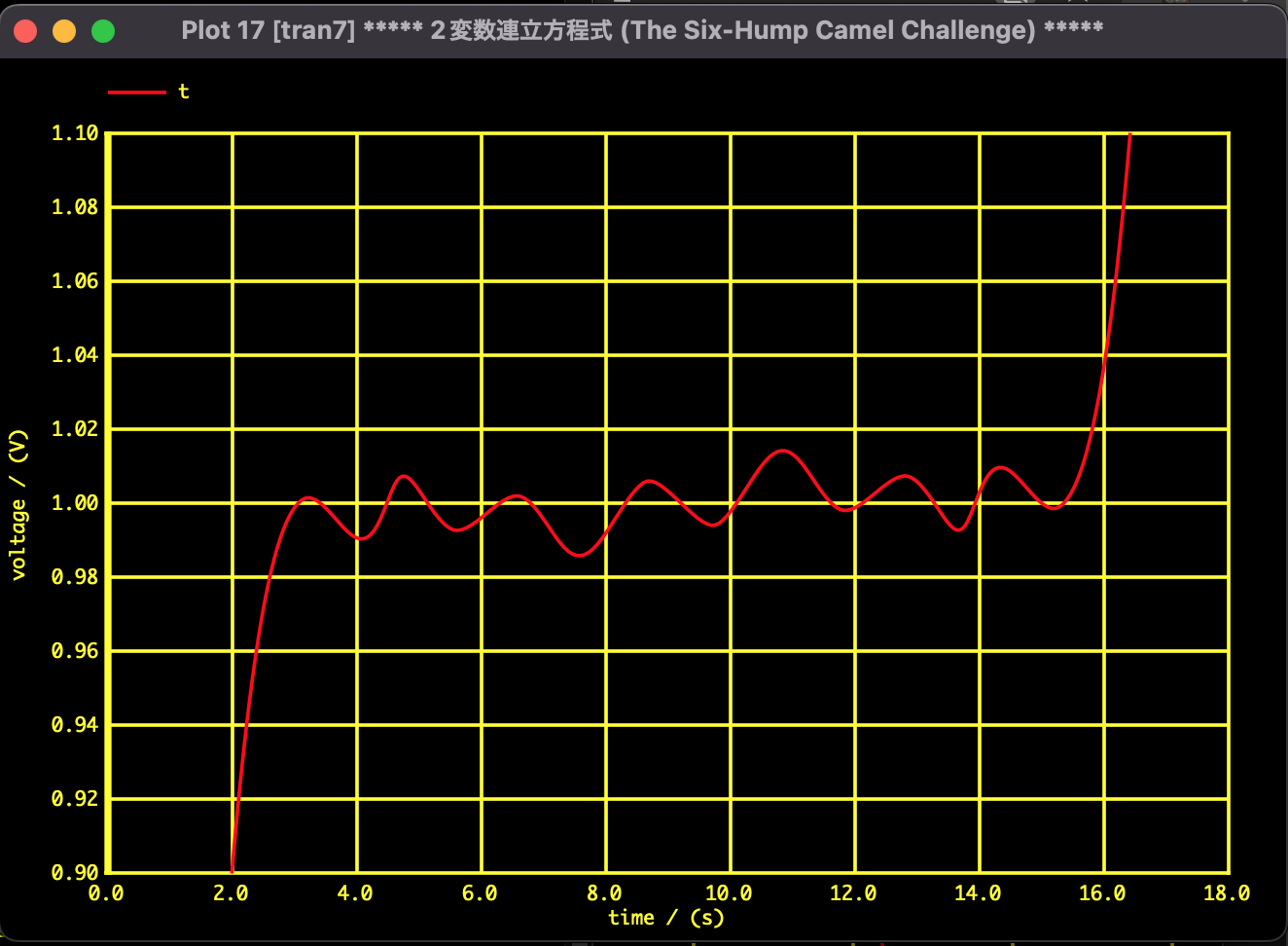
図1:横軸 時間, 縦軸 $t$。15個の解(極大・極小・鞍点)が一本の軌跡で結ばれている。
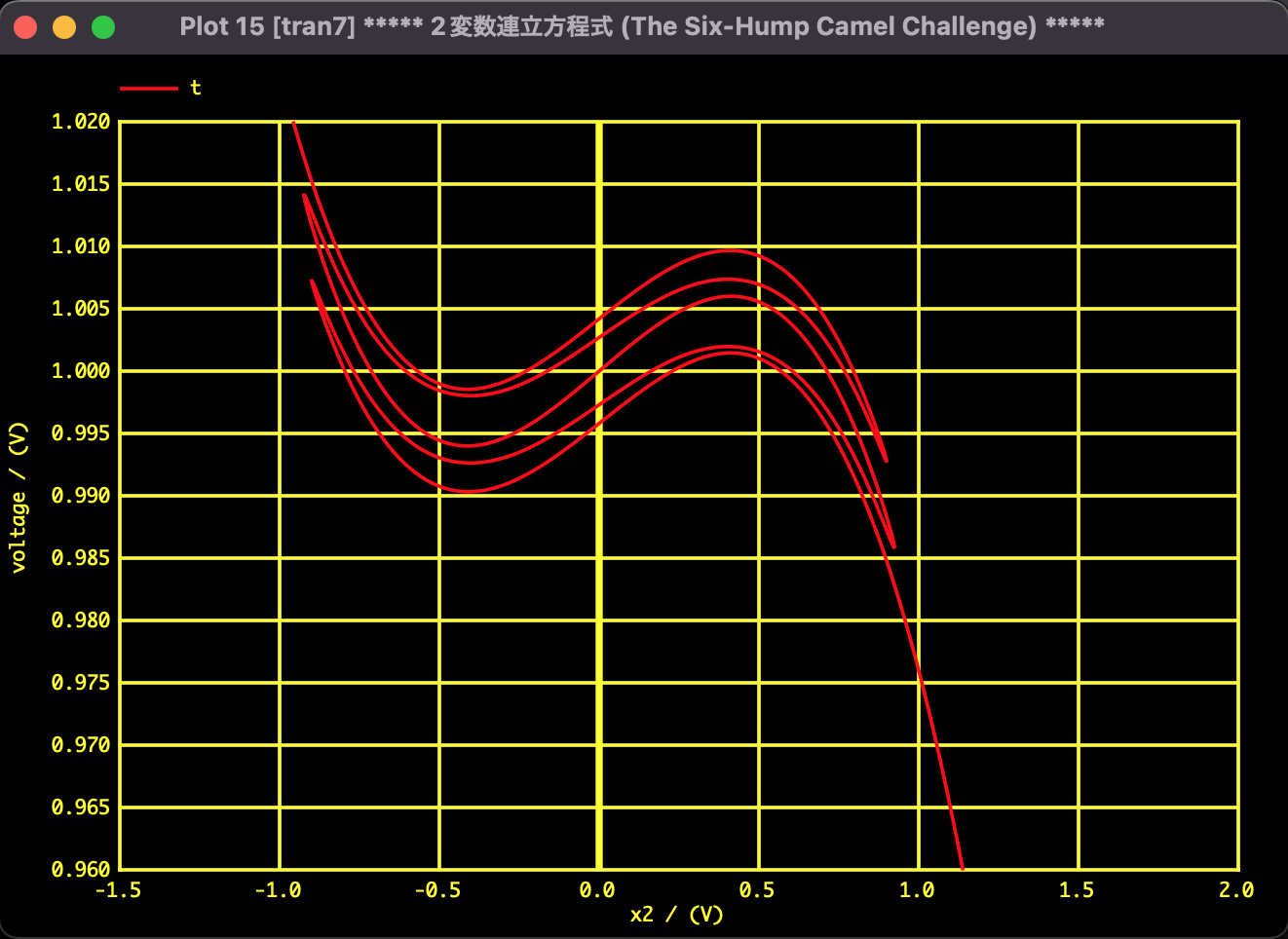
図2:横軸 $x_1$, 縦軸 $t$。解近傍の拡大図。
なお、この複雑な非線形方程式の追跡計算の実装にあたっては、一般的な数値計算プログラム(CやPython)ではなく、独自の試みとして「SPICE指向型数値解析法」を用いました。
これは、数式を電気回路のネットリストとして記述し、回路シミュレータの堅牢な過渡解析エンジンを数値ソルバーとして転用する手法です。 これにより、ホモトピー法の複雑な軌跡追跡を、安定かつ高精度に行うことができました。
5. Dr.WataWata's Insight
「連続性の中に答えがある」
ニュートン法のような「点」の探索では、孤立した解を見落としてしまいます。 しかし、ホモトピー法のように問題を「線(連続体)」として捉え直すことで、バラバラに見えていた15個の解が、実は一本の糸で繋がっていることが見えてきます。
一見無関係に見える事象も、パラメータを一つ増やして次元を上げることで、すべてが繋がった一つの物語になる。 これは数学に限らず、我々の研究や人生においても示唆に富んだ視点ではないでしょうか。