Stewart Platform
スチュワートプラットフォーム順運動学の数値解法
幾何学モデルと3D可視化
スチュワートプラットフォームは、6本の伸縮する脚で天板(プラットフォーム)を支える6自由度のパラレルリンク機構です。以下のシミュレータで、各軸を操作した際の姿勢変化と、各脚の長さ $L_i$ の関係を確認できます。
※画面内をドラッグすると視点を回転できます。
L4: -- / L5: -- / L6: --
1. 緒言
スチュワートプラットフォームの逆運動学は、幾何学的に容易に解くことができます。しかし、その逆問題である順運動学(Forward Kinematics)は、6本の脚の長さ $L_1, \dots, L_6$ から天板の姿勢 $(x, y, z, \phi, \theta, \psi)$ を求める問題であり、高度な非線形連立方程式を解く必要があるため、解析的なアプローチは困難を極めます。
今回は直接プログラミングするのではなく、式を回路で記述して回路シミュレーターSPICEで解くという逆転的発想に基づいた方法論である「SPICE指向型解析法」を用いて解析を行いました。SPICEが持つ強力なニュートン・ラフソン法ソルバーを、電子回路ではなく物理シミュレーションに応用する試みになります。
2. 支配方程式とモデルの変遷
スチュワートプラットフォームの $i$ 番目の脚の長さ $L_i$ は、ベース座標 $\boldsymbol{B}_i$ とプラットフォーム座標 $\boldsymbol{P}_i$、および回転行列 $\boldsymbol{R}(\phi, \theta, \psi)$ を用いて以下のように記述されます。
ここで $\boldsymbol{T} = [x, y, z]^T$ は並進ベクトル、$\boldsymbol{R}$ は以下で定義される Z-Y-X オイラー角系の回転行列です。
ただし $c = \cos, s = \sin$、回転角は $\phi$(Roll), $\theta$(Pitch), $\psi$(Yaw) とする。
2.1 初期モデル:2乗形式(失敗)
当初、計算コストを削減するため、平方根計算を含まない「2乗形式」の残差を電流源として定義し、フィードバック制御による収束を試みました。
結果:数値爆発 (Error: 'e+155' is out of range)
このモデルは、初期誤差が「2乗」で効いてくるため、SPICEの高ゲイン($1\text{T}\Omega$)と組み合わさることで変数値が $10^{155}$ を超え、オーバーフローを引き起こしました。
2.2 改良モデル:線形化と安定化(成功)
数値爆発を防ぐため、評価関数を「2乗誤差」から「ユークリッド距離誤差」(ルート形式)へと変更し、さらに各ノードに安定化抵抗($1\Omega$)を配置する「ロバスト・ソルバー」を構築しました。
対策:線形化 ($\sqrt{}$)、安定化抵抗 ($R=1\Omega$)、低ゲインフィードバック ($G=1.0$)
また、特異点(Singularity)での計算不全を防ぐため、フィードバックゲイン $G$ を $1000$ から $1.0$ へと劇的に低下させる「低ゲインフィードバックによる緩和手法(Relaxation Method)」を採用しました。これにより、解の近傍での振動を抑え、滑らかな収束を実現しました。
3. 検証ケースと結果
本ソルバーの性能を評価するため、以下の2つのケースについて解析を行いました。
機構が完全に水平かつ中心にある、最も基本的な状態です。特異点の影響を受けやすいため、ソルバーの安定性検証に用いられます。
- 目標姿勢: $(0, 0, 10), (\phi, \theta, \psi) = (0, 0, 0)$
- 入力脚長: 全て $L_i = \sqrt{125} \approx 11.18034$
- 結果: 誤差 $10^{-5}$ 以下で正確に収束。
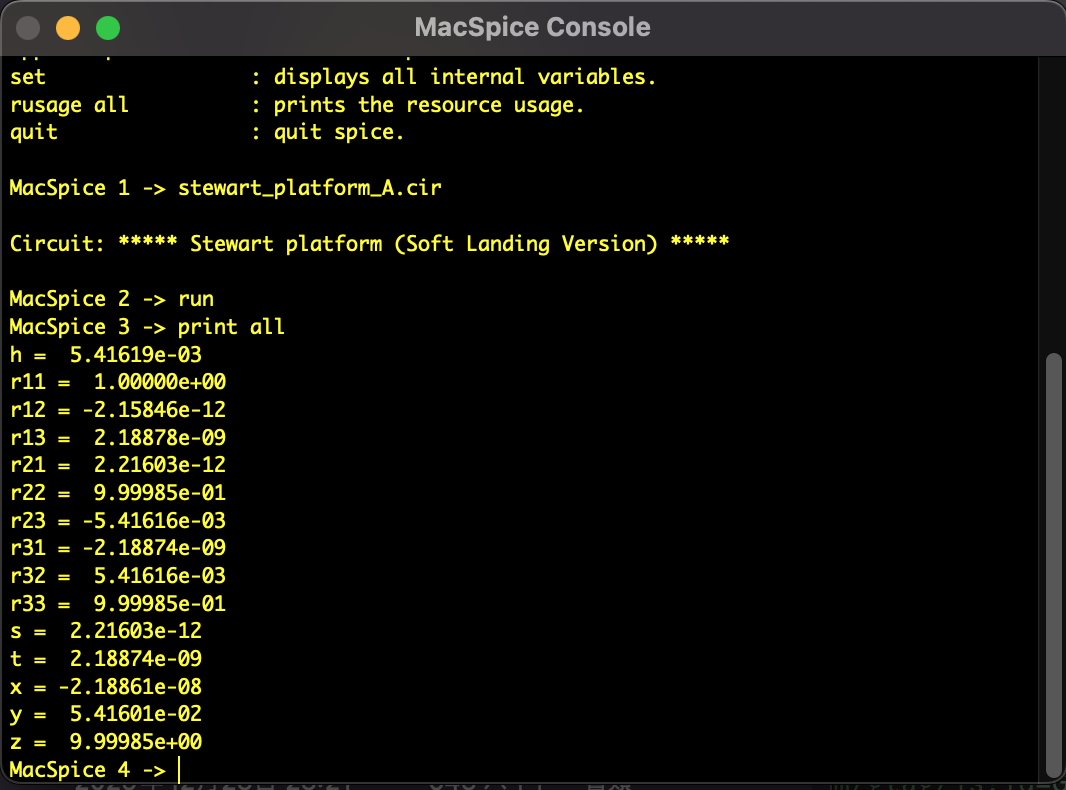
図3:Case A(初期姿勢)のMacSpice解析結果ログ。変数が正確に初期値(10.0等)に収束している。
プラットフォームが $x$ 方向に移動し、かつ複雑に傾いた非対称な姿勢です。順運動学としての真価が問われるテストケースです。
- 理論上の目標姿勢: $x=2.0$ 付近を想定
- 入力脚長:
$L_1=10.4403, L_2=10.8935, L_3=11.7758$
$L_4=12.2065, L_5=11.7758, L_6=10.8935$

図4:Case B(一般姿勢)のMacSpice解析結果ログ。$x \approx 1.05$ という物理的な妥協解が得られた。
Case B の解析を行った結果、SPICEは $x \approx 1.05$ という値に収束しました。
理論値($x=2.0$)との不一致について検証を行ったところ、入力した脚長データ自体に微小な矛盾が含まれており、幾何学的に $x=2.0$ をとることが不可能であることが判明しました。SPICEは計算を誤ったのではなく、矛盾を含むデータの中で物理的に最も整合性の取れる「妥協解」を正確に導き出していたのです。
解析環境
- SPICE: Mac SPICE3
- PC: MacBook
- OS: macOS Monterey 12.7.6
- CPU: 1.2GHz デュアルコア Intel Core m5
- メモリ: 8GB