Van der Pol Oscillator

3. ファン・デル・ポール振動子

\[ \frac{d^2x}{dt^2} - \mu (1 - x^2) \frac{dx}{dt} + x = 0 \]

Parameter: $\mu$ (Damping coefficient)

特徴

オランダの物理学者バルタザール・ファン・デル・ポールが、真空管回路（三極管発振回路）の挙動を記述するために提案した非線形微分方程式です。

この方程式の最大の特徴は、エネルギーの発散と減衰がバランスする特定の軌道、すなわち「リミットサイクル（極限閉軌道）」を持つことです。初期値がどこにあっても、最終的には必ずこの閉じた軌道に吸い寄せられ、安定した持続振動を続けます。

パラメータ $\mu$ が大きい場合、波形は正弦波から逸脱し、急激な充放電を繰り返す「弛緩振動 (Relaxation Oscillation)」と呼ばれる波形になります。

横軸に変位 $x$、縦軸に速度 $\dot{x}$ をとった位相平面上の軌跡を描画します。
スライダーでパラメータ $\mu$ を変更すると、円形（単振動）から歪んだ形（弛緩振動）へとリミットサイクルの形状が変化する様子を確認できます。

Parameter $\mu$: 1.0

図1：位相空間上の軌跡。外側からスタートしても内側からスタートしても、太線の軌道（リミットサイクル）に収束します。

ファン・デル・ポール振動子を台形法で解析した結果を示します。

今回は直接プログラミングするのではなく、式を回路で記述して回路シミュレーターSPICEで解くという逆転的発想に基づいた方法論である「SPICE指向型解析法」を用いて解析を行いました。

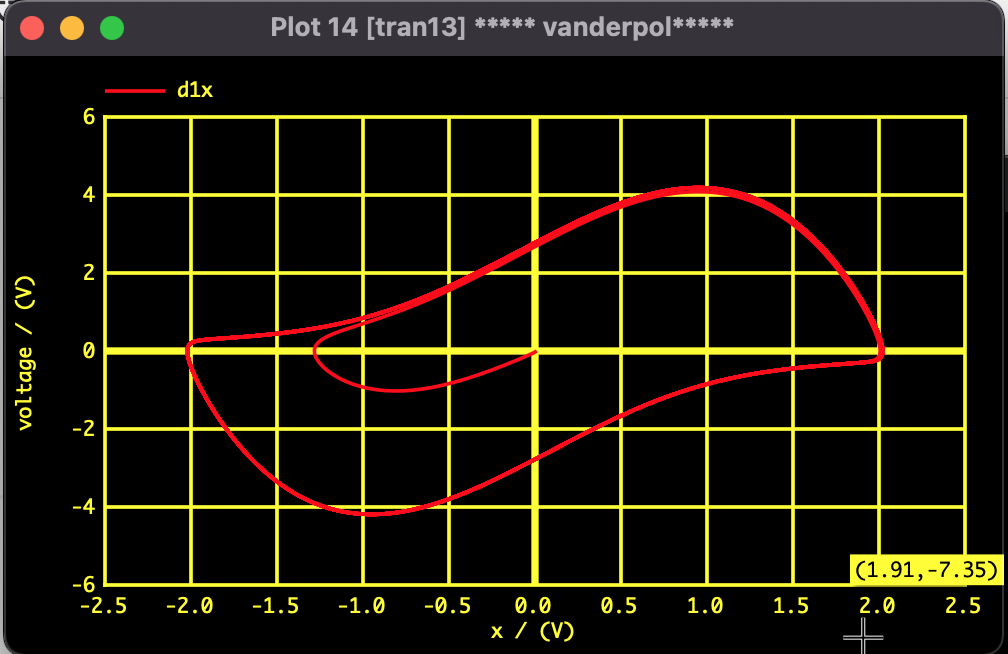
図2：SPICE指向型解析法によるファン・デル・ポール振動子の波形（時間領域）

この規模の計算では現在のPC環境であれば一瞬で収束するため、詳細な計算時間の計測は割愛いたします。