Numerical Integration for ODEs
常微分方程式の基礎とStiff系に対する安定解法
1. 微分方程式と常微分方程式 (ODE)
微分方程式 (Differential Equation) とは、ある未知関数とその導関数(変化率)の関係を記述した等式のことです。物理学における運動方程式や、電気工学における回路方程式など、自然界の動的な法則の多くはこの形で記述されます。
常微分方程式と偏微分方程式
- 常微分方程式 (Ordinary Differential Equation, ODE):
独立変数が1つ(通常は時間 $t$)のみであるもの。回路シミュレーションにおける過渡解析は主にこれを扱います。 - 偏微分方程式 (Partial Differential Equation, PDE):
独立変数が2つ以上(時間 $t$ と空間 $x, y, z$ など)あるもの。電磁界解析や流体解析などで現れます。
常微分方程式の一般式
未知関数ベクトルを $\boldsymbol{x}(t)$ とするとき、1階の常微分方程式は一般に以下の形式で表されます。
ここで $\boldsymbol{x}_0$ は初期値です。数値解析の目的は、この初期値から出発して、時間刻み幅 $h$ ごとの数列 $\boldsymbol{x}_1, \boldsymbol{x}_2, \dots$ を求めることです。
2. Stiff(硬い)方程式の問題
回路解析などにおいて、時定数が極めて小さい(速い)素子と大きい(遅い)素子が混在する系をStiff(硬い)方程式と呼びます。
一般的な陽解法(前進オイラー法やルンゲ・クッタ法)では、系の最も速い変化に追従するために時間刻み幅 $h$ を極限まで小さくする必要があり、計算時間が爆発的に増大します。これを解決するのが、以下に紹介する陰解法 (Implicit Method) です。
3. 台形法 (Trapezoidal Method)
微分の平均値を用いて次ステップを推定する、2次の陰解法です。
特徴:
- A-安定 (A-Stable): 複素平面の左半面すべてで計算が発散しません。
- 数値振動 (Ringing): 減衰特性が弱いため、急峻な変化点で真値を挟んで振動する現象(台形法振動)が発生します。
4. GEAR法 / 後退微分公式 (BDF)
過去の複数の解点を用いて多項式近似を行う多段法です。C.W.Gearにより提唱され、回路シミュレータの標準解法となっています。
特徴:
- L-安定 (L-Stable): 高周波成分(無限遠の固有値)を速やかに減衰させるため、Stiffな系での数値振動を強力に抑制します。
- 次数と精度: 次数 $k$ を上げることで高精度化できますが、安定性とのトレードオフが生じます。
5. 安定領域と次数の数理
数値解法の安定性は、複素平面上での絶対安定領域によって評価されます。
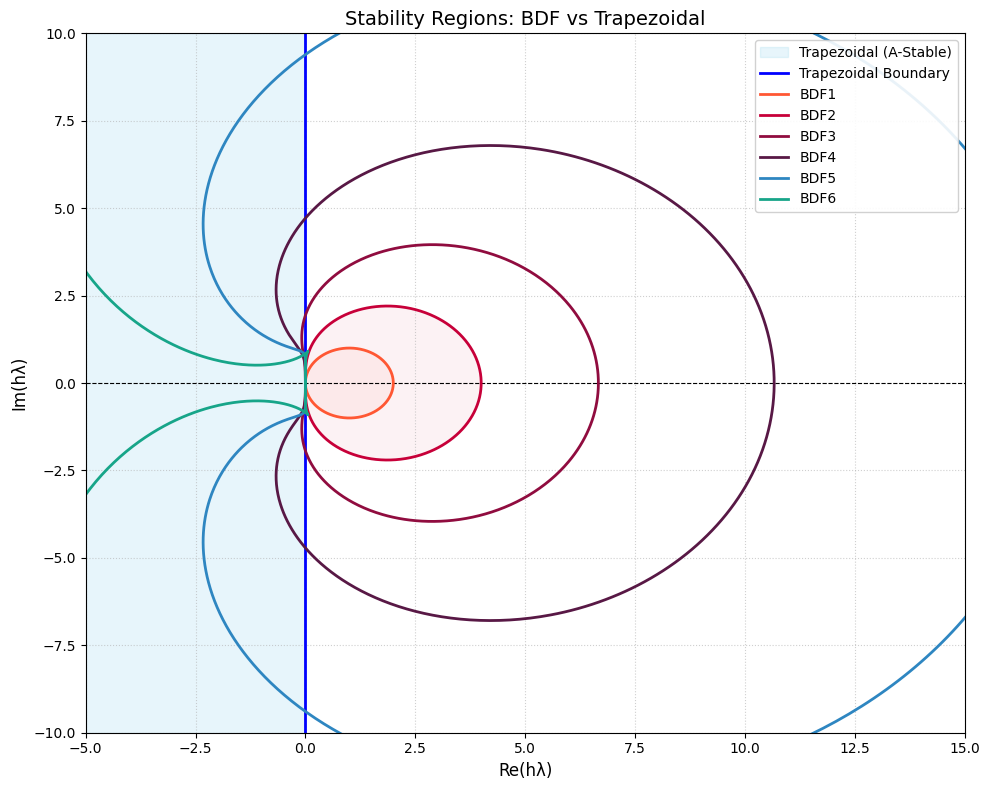
Fig 1. 複素平面 $h\lambda$ における安定領域の比較
陽解法(Runge-Kutta等)とは異なり、BDF法のような陰解法の安定領域は、描かれた境界線の「外側 (Exterior)」となります。
- Trapezoidal: 左半面(Re < 0)すべてが安定領域です(A-安定)。
- BDF 1-6: 閉曲線(不安定領域)の外側すべてが安定領域です。
Dahlquistの障壁 (Dahlquist's Barrier)
図において、BDF3以上の次数では不安定領域(閉曲線)が左半面にはみ出し、虚軸付近で安定性が失われていることが確認できます。これは「2次を超える精度の多段陰解法はA-安定になり得ない」という数学的定理による限界です。
| 次数 (Order) | 安定性 | 適応領域 |
|---|---|---|
| 1次 (Backward Euler) | L-Stable (A-Stable) | 極めてStiffな初期過渡応答 |
| 2次 (GEAR2 / Trapezoidal) | L-Stable / A-Stable | 汎用的なシミュレーション |
| 3次〜6次 (GEAR3-6) | Stiff Stable (Not A-Stable) | 高精度が必要だが、極端な振動成分を含まない系 |
6. Dr.WataWata's Insight
回路シミュレータの実装において、数値積分法は単なる数式ではなく、誤差判定による「歩幅制御 (Time-step Control)」とセットで機能するエンジンです。
台形法はエネルギー保存性が良いため発振回路の解析に適していますが、スイッチング電源のような急峻な減衰が必要な系では、L-安定性を持つGEAR法(特に2次)が圧倒的なパフォーマンスを発揮します。ツール任せにせず、解析対象の物理的特性に合わせて手法(Method)と次数(Order)を選択する視点が、エンジニアには求められます。