非線形方程式を解く有名な方法の一つにニュートン法があります。この方法は、任意に決めた初期値から反復計算を繰り返して目的とする解を求める方法です。非常に有名な方法なので、数値計算系の書籍には大概概要が詳しく記載されていますし、Web上にもたくさんの情報が掲載されています。それだけ多くの情報があるため、ニュートン法の理論的な内容に関しては 簡単に見つける事が可能です。また、1変数の非線形方程式に関しては例題を使って具体的に計算手順が示されているものが多くあります。
一方、多変数の非線形方程式に関する例題を使った具体的な計算手順はあまり記載されているものがないと感じています。
恐らく、多変数になると急激に計算量が増えるため掲載するのが面倒というのが理由ではないかと勝手に感じています。
ここで数値計算法のプログラミングを考えた場合、書籍などに記載されている理論的な内容を見ながらプログラミングをするよりも、具体的な例題を手計算で解き、その手順を見ながらプログラムを組む方がやり易いのではないかと思います。
よって、このページではニュートン法の理論的な内容を記載するのではなく(他のページなどを見てください)、ニュートン法を使って多変数の非線形方程式を手計算で解く場合の計算手順を記載したいと思います。なお、理論的な内容はこのサイト
がすっきりまとまっていて分かりやすいのではないかと思います。
まず、解くべき非線形方程式は以下とします(2変数です)。
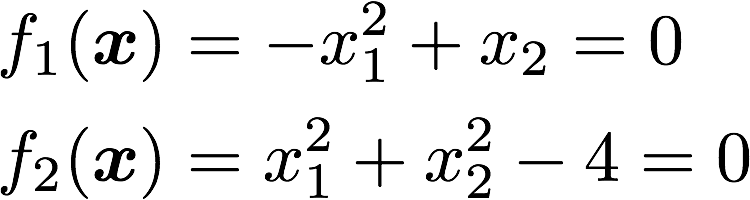
この式のヤコビ行列を考えると以下のようになります。
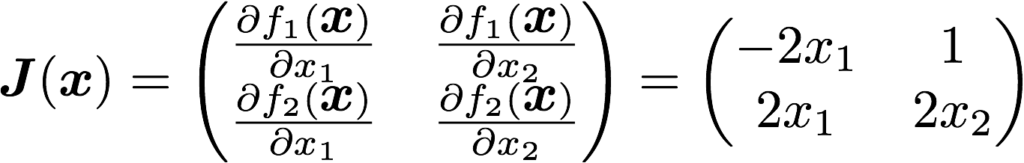
kステップ目の近似値をxkとすると、ニュートン法の計算式は以下のようになります。この式は多くの書籍やサイトに記載されているので詳しくはそちらを参照してください。
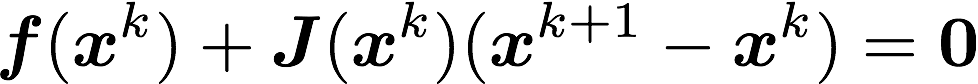
要するに、ニュートン法はこの式を使って反復計算を行えば解を得られる訳です。ただ、注意が必要でこの式を解く場合、ヤコビ行列の逆行列を求めて解こうとすると計算時間が掛かってしまいます(逆行列の計算はコンピュータで時間がかかる)。よって、一般的にニュートン法はヤコビ行列の逆行列を求める事はせず、この式を連立1次方程式とみなして、LU分解やガウスの消去法などを適用して解く事になります。
それではニュートン法の計算式に今回解くべき非線形方程式をあてはめると、反復計算で解く連立1次方程式は以下のようになります。
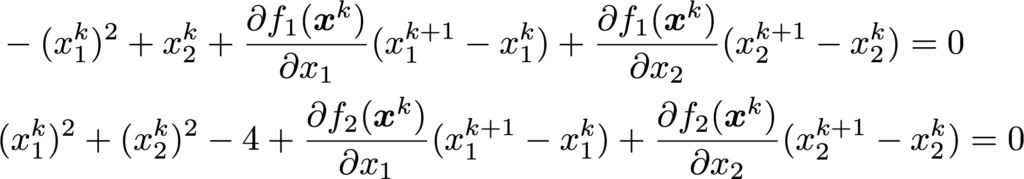
↓
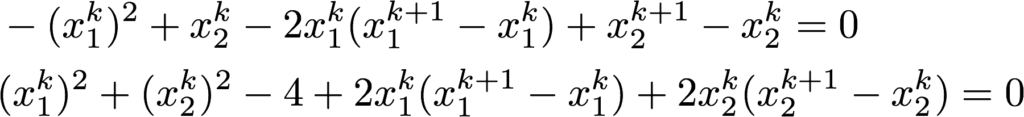
ちょっと式がぐちゃぐちゃして分かり難いので以下のように置きます。
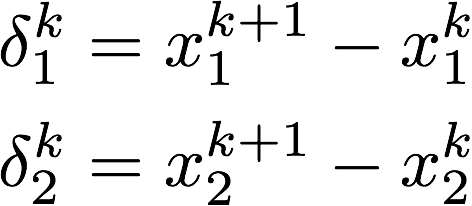
そうしますと最終的に解くべき式は以下になる訳です。
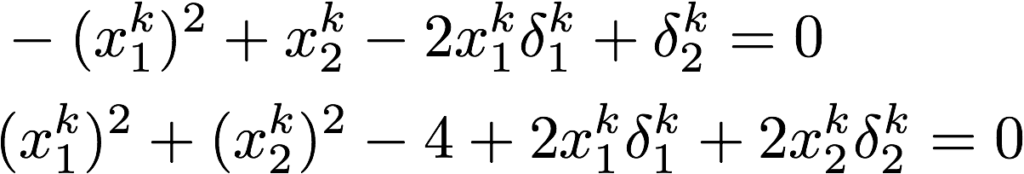
変数を以下の2つとする連立1方程式という事になります。
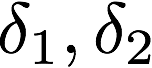
それではこの式を解いていきます。連立1次方程式の解法としてはLU分解を採用しました。LU分解の具体的な計算手順は他ページを確認してください。
●ステップ k=1
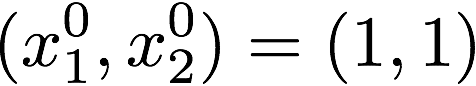
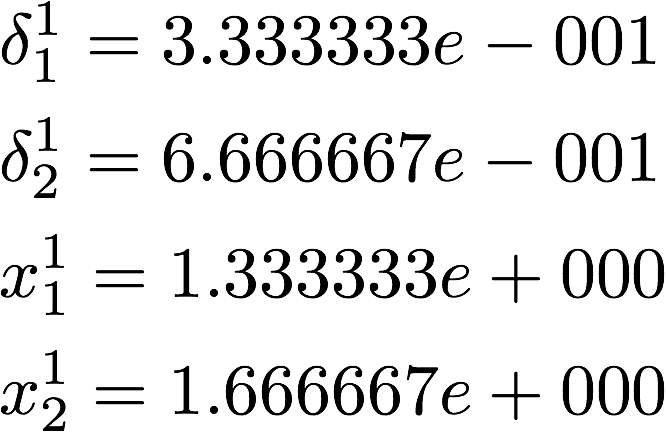
●ステップ k=2
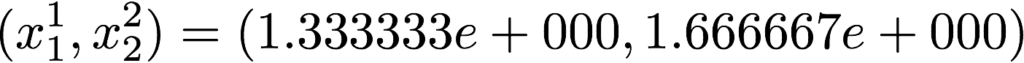
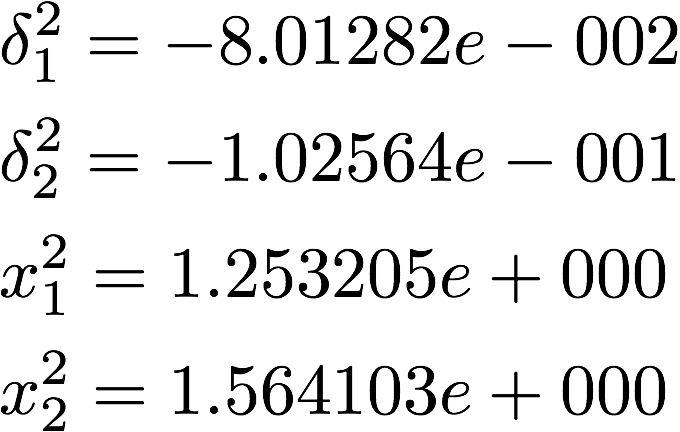
●ステップ k=3
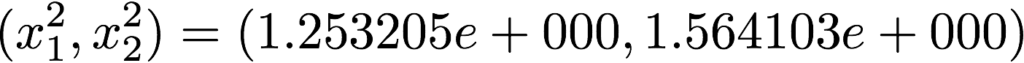
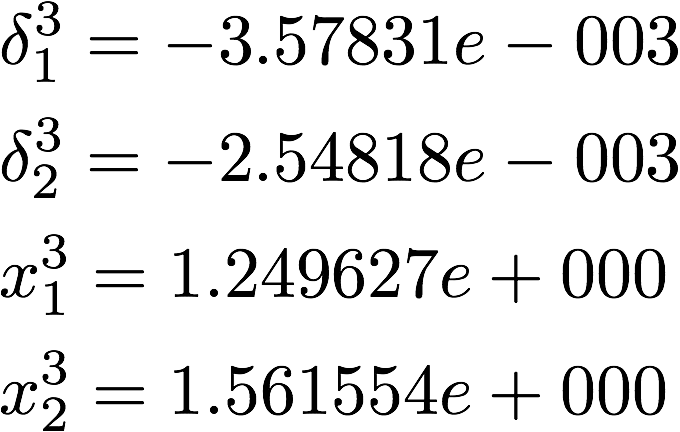
●ステップ k=4
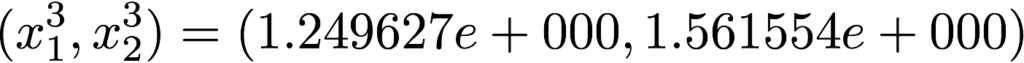
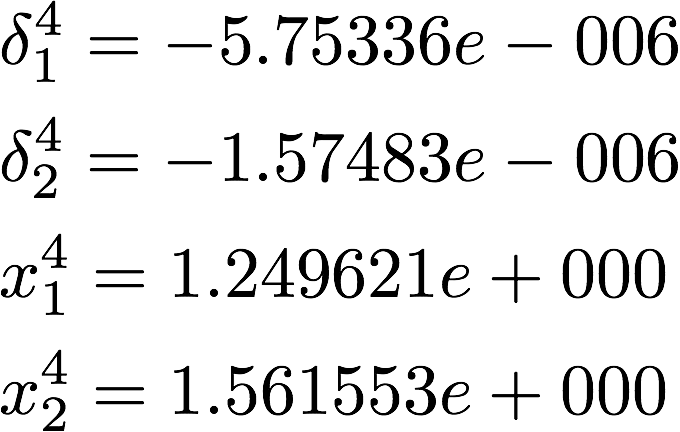
上記のように反復計算を続けて行くと以下の値に収束し、2変数非線形方程式の解を得る事が出来ます。反復の計算の停止条件は色々ありますが、その辺は他サイトを見てください。
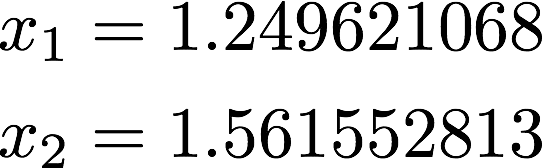
なお、ニュートン法の説明に関しては、数値計算のような専門書も役に立ちますが、意外と以下の電子回路シミュレーションに関する書籍が分かりやすいのではないかと思います。是非活用して見てください。


